Remarques

$\imath-$ Le crochet de Poisson est une notion purement algébrique, et donc plus fondamentale que le crochet de Poisson classique, défini par référence à un ensemble de coordonnées, et il existe des observables spécifiquement quantiques (tel le spin) sans analogue classique.

$\imath\imath-$ Nous remarquons que deux variables $P_i$ et $Q_j$ avec $i\not=j$ commutent toujours, et que, par suite, toute fonction des $P_i$ et des $Q_i$ commute toujours avec toute fonction des $Q_j$ et $P_j$ si $j\not=i$ . Or, les indices $i$ et $j\ldots$ repèrent des degrés de liberté. On peut donc dire que des variables dynamiques ou des observables relatives à des degrés de liberté différents, commutent toujours entre elles.

$\imath\imath\imath-$ Il y a lieu de remarquer que la notion d'E.C.O.C. peut être considérée comme une transposition quantique de la notion classique de degré de liberté. En effet, le nombre des degrés de liberté d'un système classique est égal au nombre minimum de paramètres indépendants nécessaires pour définir sans ambiguïté l'état de ce système. Les valeurs de ces paramètres sont celles d'un ensemble de grandeurs physiques (par exemple $\hat{X},\hat{Y},\hat{Z},\hat{P_x},\hat{P_y},\hat{P_z}$ ) indépendantes et en fonction desquelles au contraire s'expriment toutes les autres, et par exemple :

$$\hat{L_x}=\hat{Y}\,\hat{P_z}-\hat{Z}\,\hat{P_y}~~~~~~~~~ \hat{H}=\frac{1}{2M}\,\hat{{\vec{P}}}^{\,2}+V\left(\hat{X},\hat{Y},\hat{Z}\right)$$

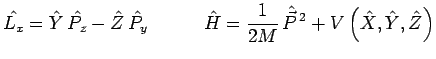D'une manière générale, le nombre d'observables nécessaires pour constituer un E.C.O.C. est égal un nombre minimum d'observables indépendantes nécessaires pour que leurs vecteurs propres communs définissent sans ambiguïté des états physiques bien définis. Le nombre de ces observables nécessaires dépend du degré de dégénérescence de leurs valeurs propres et donc dépend du choix de ces observables. Puisque pour chaque degré de liberté, $X$ et $P_x$ ne commutent pas, il en résulte qu'en général ce nombre d'observables nécessaires est au moins égal à la moitié du nombre classique de degrés de liberté.

$\imath v-$ Si les commutateurs ne sont pas nuls en général, c'est parce qu'ils sont fonctions de la constante fondamentale $\hbar$ qui n'est pas nulle. Cette constante a toutefois une valeur très faible (faible signifiant ici par rapport aux grandeurs de même nature, à notre échelle) ainsi que l'atteste sa valeur numérique exprimée dans l'unité Joule $\times$ seconde, adaptée aux phénomènes à notre échelle :

$$\hbar=1,05.10^{-34}~~\mathrm{Joule}\times\mathrm{seconde}$$

Faire comme si $\hbar=0$ c'est faire comme si tous les commutateurs étaient nuls et c'est alors dans une certaine mesure retrouver la mécanique classique. Ainsi, selon Dirac, la mécanique classique peut être considérée comme le cas limite de la mécanique quantique quand $\hbar$ tend vers zéro. On retrouve ici une situation analogue à celle de la théorie de la relativité. Considérer la constante $c$ (vitesse des particules de masse nulle) comme infinie alors que sa valeur est seulement très grande :

$$c\simeq 3.10^8~~m.s^{-1}$$

c'est faire l'approximation classique^III3.

Ainsi, la mécanique classique est une approximation à la fois non quantique ( $\hbar\not=0$ ) et non relativiste ( $c\not=\infty$ ).