Remarque :

On notera que les transformations $G(\vec{V},t)$ de Galilée qui viennent d'être considérées sont des transformations qui peuvent être appelées actives dans le sens suivant :

  $\bullet$   Si la grandeur physique $\hat{A}$ est mesurée avec un appareillage $\cal A$ lié au référentiel $\Sigma$ , la grandeur physique $\hat{A}^\prime$ telle que $A^\prime = G\,A\,G^{-1}$ est celle qui est mesurée par le même appareillage $\cal A$ mais, mis en mouvement uniforme, et lié au référentiel $\Sigma^\prime$ .

  $\bullet$   De même, si l'état $K$ est préparé avec un appareillage $\cal K$ lié au référentiel $\Sigma$ , l'état $K^\prime$ tel que $\mid K^\prime> = G\,\mid K>$ ets l'état qui est préparé par le même appareillage $\cal K$ mais, mis en mouvement uniforme, et lié au référentiel $\Sigma^\prime$ .

  $\bullet$   La transformation $G(\vec{V},t)$ ne réalise donc pas ici un changement de référentiel $\Sigma~\rightarrow~\Sigma^\prime$ mais un changement d'état $K~\rightarrow~K^\prime$ et un changement d'observable $A~\rightarrow~A^\prime$ .

Question 3-26 : Montrez explicitement comment passer de l'expression de $g(t)$ à celle de $G(V,t)$ puis à celle de $G(\vec{V},t)$ .

Question 3-27 : En utilisant l'expression explicite de G démontrez :

$$X^\prime = G\,X\,G^{-1} \,=\, X - V\,t$$

$$P_x^\prime = G\,P_x\,G^{-1} \,=\, P_x - M\,V$$

$$H^\prime = G\,H\,G^{-1} \,=\, H-\vec{V}\,\vec{P} + \frac{1}{2}\,M\,\vec{V}^2$$

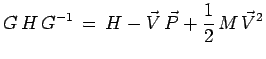Nota-Bene : On pourra utiliser la relation mathématique générale :

$$e^\Omega\,A\,e^{-\Omega} = A + [\Omega,A] + \frac{1}{2!}\,[\Omega,[\Omega,A]]+\frac{1}{3!}\,[\Omega,[\Omega,[\Omega,A]]]+\ldots$$

$\Omega$ et A désignant deux opérateurs qui en général ne commutent pas.

Question 3-28 : Soit $\vec{p}$ et $\lambda$ l'impulsion et la longueur d'onde associée d'une particule dans S. Calculez $\vec{p}^{\,\prime}$ et $\lambda^\prime$ mesurées dans $S^\prime$ et vérifiez les relations simultanées :

$$p = \frac{h}{\lambda}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~p^\prime~=~\frac{h}{\lambda^\prime}$$

Nota-Bene : On pourra utiliser la relation mathématique générale :

$$e^{A+B} = e^A\,e^B\,e^{-\frac{1}{2}\,[A,B]}$$

A et B désignant deux opérateurs quelconques.