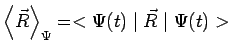Remarque

L'équation précédente dit que la position moyenne de la particule, qui est bien définie à chaque instant :

$$\left<\vec{R}\right>_\Psi=<\Psi(t)\mid \vec{R}\mid \Psi(t)>$$

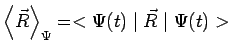se déplace en décrivant donc une trajectoire, comme si cette particule était soumise à une force $\vec{F}$ . Toutefois, tandis que dans la mécanique classique cette force est définie en chaque point $M$ par la valeur locale en ce point des dérivées partielles du potentiel :

$$\vec{F}_\mathrm{classique}=-\,\overrightarrow{\mathrm{grad}}\,V$$

dans l'équation précédente la valeur de la force en $M$ fait intervenir la valeur du potentiel dans tout l'espace :

$$\vec{F}=-\int_{-\infty}^{+\infty}\,\Psi^*(\vec{r},t). \overrightarrow{\mathrm{grad}}\,V(\vec{r}).\Psi(\vec{r},t)\,d^3r$$

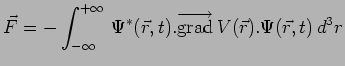Il n'y a pas lieu de s'en étonner puisque la position moyenne fait précisément intervenir toutes les positions possibles de la particule dans tout l'espace.

Toutefois, dans le cas très particulier d'un potentiel harmonique :

$$V=\frac{1}{2}\,k\,\vec{R}^2~~~~~~~~~\overrightarrow{\mathrm{grad}}\,V=k\,\vec{R}$$

on a :

$$\vec{F}=-k\int_{-\infty}^{+\infty}\,\mid \Psi(\vec{r})\mid ^2\,\vec{r}\,d^3r= -k\,\left<\vec{R}\right>_\Psi$$

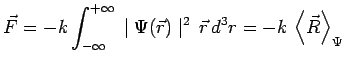et alors la position moyenne :

$$\left<\vec{R}\right>_\Psi=<\Psi(t)\mid \vec{R}\mid \Psi(t)>=\vec{r}(t)$$

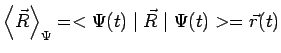se déplace bien conformément à l'équation de Newton :

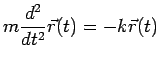$$m\frac{d^2}{dt^2}\vec{r}(t)=-k\vec{r}(t)$$