Pour un système isolé, sans interaction avec d'éventuels champs de force
extérieurs, l'expression classique de son énergie totale ne dépend que des
variables internes du système (distances relatives entre les composantes du système)
et des variables qui décrivent son mouvement (impulsion du centre de masse et
rotation autour de ce centre de masse). Cette expression ne dépend pas des
coordonnées ![]() de ce centre de masse et donc l'opérateur quantique
hamiltonien
de ce centre de masse et donc l'opérateur quantique
hamiltonien ![]() n'en dépend pas non plus. Pour un tel système l'espace est
homogène et l'expression de son hamiltonien est invariante par translation de
telle sorte que :
n'en dépend pas non plus. Pour un tel système l'espace est
homogène et l'expression de son hamiltonien est invariante par translation de
telle sorte que :
et pour une translation infinitésimale (avec
![]() ) :
) :
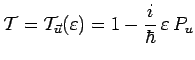 |
![]() désignant la composante dans la direction
désignant la composante dans la direction ![]() de
l'impulsion totale du système :
de
l'impulsion totale du système :
Quelle que soit la direction ![]() , la composante
, la composante ![]() est une constante du
mouvement, et en particulier :
est une constante du
mouvement, et en particulier :
Question 4-5 : Donnez des exemples de systèmes isolés. Ecrivez leurs hamiltoniens et montrez qu'ils sont invariants par translation. Donnez un exemple de système non isolé. Ecrivez son hamiltonien et montrez que l'impulsion totale n'est plus une constante du mouvement.