c) Deux particules de spin $s_1$ et $s_2$

Dans ce cas, un E.C.O.C. de l'espace complet des états sera, par exemple, constitué des observables :

$$X_1,Y_1,Z_1,X_2,Y_2,Z_2,\vec{S_1}^2,S_{1z},\vec{S_2}^2,S_{2z}$$

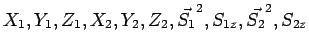avec :

$$\vec{S_1}^2=s_1\,(s_1+1)\,\hbar^2~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{et}~~~~~~~~~~~~~~~~~~~~~~~~ \vec{S_2}^2=s_2\,(s_2+1)\,\hbar^2$$

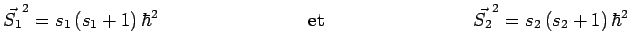correspondant à la décomposition de l'espace des états :

$$\mathcal{H}= \mathcal{H}^0_1\otimes\,\mathcal{H}^0_2\otimes\, \mathcal{H}^s_1\otimes\,\mathcal{H}^s_2$$

et un état pourra être représenté, par exemple, par un vecteur ket de la forme :

$$\mid \Psi>\,=\Psi_1^0(x_1,y_1,z_1)\,\Psi_2^0(x_2,y_2,z_2)\,\mid s_1,m_1>\otimes\,\mid s_2,m_2>$$

dont la signification est maintenant évidente.

De même que dans l'espace $\mathcal{H}^0_1\otimes\,\mathcal{H}^0_2$ les états ne sont pas nécessairement factorisables comme dans l'exemple précédent :

$$\Psi_{\mathrm{qcq}}^0(\vec{r_1},\vec{r_2})\not= \Psi_1^0(\vec{r_1}).\Psi_2^0(\vec{r_2})$$

de même dans l'espace des états de spin $\mathcal{H}^s_1\otimes\,\mathcal{H}^s_2$ , un état de spin quelconque $\mid \mathrm{spin~qcq}>$ n'est pas non plus factorisable :

$$\mid \mathrm{spin~qcq}>\not=\mid s_1,m_1>\otimes\,\mid s_2,m_2>$$

Précisément dans le sous-chapitre suivant, nous allons apprendre à construire de tels états de spin dans l'espace :

$$\mathcal{H}^s=\mathcal{H}^s_1\otimes\,\mathcal{H}^s_2$$