Si deux observables ![]() et
et ![]() commutent, elles admettent un ensemble complet de
vecteurs propres communs et réciproquement :
commutent, elles admettent un ensemble complet de
vecteurs propres communs et réciproquement :
Réciproque : Si
![]() est
complet
est
complet
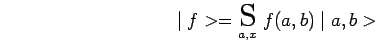
![$ ~~[A,B]\mid f>=\underset{a,x}{\scalebox{1.7}{S}}~f(a,b)[A,B]\mid a,b>$](img342.png)
Proposition directe : Si ![]()
![]() est une observable et ses vecteurs propres
est une observable et ses vecteurs propres ![]() constituent donc un système complet. En particulier pour tout vecteur
propre de
constituent donc un système complet. En particulier pour tout vecteur
propre de ![]() on a :
on a :
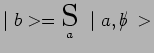
![]() désignant la projection de
désignant la projection de ![]() dans
dans
![]()
![]() de telle sorte que dans la somme du second
membre, chaque valeur propre de
de telle sorte que dans la somme du second
membre, chaque valeur propre de ![]() n'apparait qu'une seule
fois au plus. Par ailleurs :
n'apparait qu'une seule
fois au plus. Par ailleurs :
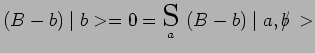
Or, chacun des vecteurs de la somme du second membre est un vecteur propre de
![]() car :
car :
Par suite, ce second membre est une combinaison linéaire de vecteurs propres
de ![]() relatifs à des valeurs propres distinctes (puisque chacun n'apparait au
plus qu'une seule fois) donc orthogonaux entre eux et ainsi linéairement
indépendants. Puisque cette somme est nulle, chacun de ses termes est
lui-même nul.
relatifs à des valeurs propres distinctes (puisque chacun n'apparait au
plus qu'une seule fois) donc orthogonaux entre eux et ainsi linéairement
indépendants. Puisque cette somme est nulle, chacun de ses termes est
lui-même nul.
![]() est donc vecteur propre de
est donc vecteur propre de ![]() relatif à la
valeur propre
relatif à la
valeur propre ![]() et par suite on peut écrire,
et par suite on peut écrire, ![]() désignant un vecteur normé :
désignant un vecteur normé :
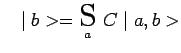
Par ailleurs, puisque les vecteurs propres de l'observable ![]() forment un système complet, tout vecteur ket
forment un système complet, tout vecteur ket ![]() est
développable selon une base
est
développable selon une base
![]() :
:
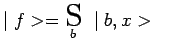 et
et
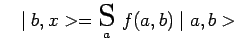
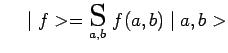
et
![]() constitue bien un ensemble complet de
vecteurs propres communs de
constitue bien un ensemble complet de
vecteurs propres communs de ![]() et
et ![]() .
.
Plus généralement, si ![]() observables
observables ![]() etc, commutent deux à
deux, ces
etc, commutent deux à
deux, ces ![]() observables admettent un système complet de vecteurs propres communs
:
observables admettent un système complet de vecteurs propres communs
:
dont chacun, quand ![]() augmente, est de mieux en mieux repéré par
les
augmente, est de mieux en mieux repéré par
les ![]() valeurs propres simultanées auxquelles il est associé. On peut
démontrer qu'il est possible de choisir un nombre maximum
valeurs propres simultanées auxquelles il est associé. On peut
démontrer qu'il est possible de choisir un nombre maximum ![]() de telles
observables
de telles
observables
![]() indépendantesI28et qui commutent deux à deux, de telle sorte qu'à tout ensemble de valeurs
propres simultanées ne corresponde qu'un seul vecteur propre commun, défini
à un facteur près :
indépendantesI28et qui commutent deux à deux, de telle sorte qu'à tout ensemble de valeurs
propres simultanées ne corresponde qu'un seul vecteur propre commun, défini
à un facteur près :
|
Il y a lieu de remarquer que chacun des vecteurs propres
![]() d'un E.C.O.C., même s'il est normé, n'est
déterminé qu'à un facteur de phase
d'un E.C.O.C., même s'il est normé, n'est
déterminé qu'à un facteur de phase
![]() près avec
près avec
![]() . En ce sens, la base mathématique
de
. En ce sens, la base mathématique
de
![]() demeure elle-même indéterminée. Cette situation
paraît sans conséquence physique puisqu'il s'agit d'une simple
base mathématique arbitraire dans un espace
vectorielI29.
demeure elle-même indéterminée. Cette situation
paraît sans conséquence physique puisqu'il s'agit d'une simple
base mathématique arbitraire dans un espace
vectorielI29.
Question 1-13 : Soit
![]() l'ensemble des
vecteurs propres d'un opérateur hermitique
l'ensemble des
vecteurs propres d'un opérateur hermitique ![]() , dont les valeurs
propres
, dont les valeurs
propres ![]() , non dégénérées, constituent un spectre
discret. On considère l'ensemble des opérateurs :
, non dégénérées, constituent un spectre
discret. On considère l'ensemble des opérateurs :
![]() Montrez que
Montrez que ![]() satisfait une équation algébrique et en
déduire que
satisfait une équation algébrique et en
déduire que ![]() est une observable dont on déterminera les vecteurs
propres et les valeurs propres.
est une observable dont on déterminera les vecteurs
propres et les valeurs propres.
![]() Montrez que la base
Montrez que la base
![]() est bien
constituée des vecteurs propres communs d'un E.C.O.C. que l'on
déterminera.
est bien
constituée des vecteurs propres communs d'un E.C.O.C. que l'on
déterminera.