a) Etats indiscernables

Si donc nous considérons un système constitué seulement de telles particules identiques, les deux conséquences suivantes vont notamment en résulter.

$\imath-$ Deux états du système, qui ne différeraient l'un de l'autre que par un échange entre deux de ces particules, ou plus généralement, par une permutation quelconque entre ces particules, sont indiscernables, c'est-à-dire qu'ils ne peuvent être distingués l'un de l'autre, et qu'ils ne constituent en fait qu'un seul et même état.

$\imath\imath-$ Toute transition du système physique, qui ne consisterait qu'en un échange entre deux ou plusieurs de ces particules, est inobservable expérimentalement. En fait, il n'y a eu ni changement d'état, ni transition.

Une théorie satisfaisante, c'est-à-dire qui rend compte des observations expérimentales, ne doit ni distinguer les états physiques, qui ne sont pas différents, ni décrire des processus inobservables, et donc qui n'en sont pas non plus. Or nous allons constater que le formalisme quantique, tel qu'il a été développé jusqu'ici, ne satisfait pas cette exigence. Ce formalisme va donc devoir être corrigé ci-après, et ce sera le rôle du principe de Pauli.

L'échange de deux particules identiques n'a aucune signification physique, et pourtant le formalisme quantique lui en donne un. En effet, considérons d'abord pour simplifier un système à deux particules identiques et un état représenté par la fonction d'onde :

$$\Psi(\vec{r}_1,\vec{r}_2)=\varphi_\alpha(\vec{r}_1).\varphi_\beta(\vec{r}_2)= <\vec{r}_1\mid \alpha><\vec{r}_2\mid \beta>$$

et donc tel que la particule 1 est dans l'état $\mid \alpha>$ et la particule 2 dans l'état $\mid \beta>$ . Echanger les deux particules, c'est les permuter. A cette permutation $P(1,2)$ correspond dans l'espace des états un opérateur de permutation induite noté $\mathcal{P}(1,2)$ tel que :

$$\mathcal{P}(1,2)\,\Psi(\vec{r}_1,\vec{r}_2)=<\vec{r}_2\mid \alpha><\vec{r}_1\mid \beta>= \Psi(\vec{r}_2,\vec{r}_1)$$

et bien évidemment :

$$\Psi(\vec{r}_2,\vec{r}_1)\not=\Psi(\vec{r}_1,\vec{r}_2)$$

Par exemple :

$$(1+\vec{r}_1^2)^{-\frac{1}{2}}\,e^{-\beta\,\vec{r}_2^2}\not= (1+\vec{r}_2^2)^{-\frac{1}{2}}\,e^{-\beta\,\vec{r}_1^2}$$

Plus généralement, pour un système composé de $n$ particules identiques, si $P$ désigne une permutation des $n$ particules dans l'espace physique à trois dimensions, et par exemple :

$$P=\left(\begin{array}{ccccc} 1 & 2 & 3 & \ldots & n \\ i & j & k & \ldots & z \\ \end{array}\right)$$

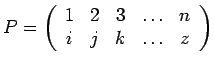l'opérateur de permutation induite correspondant $\mathcal{P}$ aura pour effet, dans l'espace des états :

$$\mathcal{P}\,\Psi(\vec{r}_1,\vec{r}_2,\ldots,\vec{r}_n)= \Psi(\vec{r}_i,\vec{r}_j,\ldots,\vec{r}_z)$$

Ainsi une permutation des particules doit être codée dans le formalisme par la même permutation, effectuée sur les coordonées, dans la fonction d'onde. Or, bien évidemment pour une fonction d'onde générale et donc quelconque (mais normée) :

$$\mathcal{P}\,\Psi\not=\Psi$$

Ainsi par permutation des particules, la représentation mathématique de l'état change, sans que cet état physique n'ait lui-même changé ! Nous allons même constater qu'à un même état physique peut correspondre $n!$ vecteurs kets linéairement indépendants.