En raison de l'isotropie de l'espace, pour un système fermé, le moment angulaire
total ![]() d'un ensemble de plusieurs particules est une constante du mouvement
qui commute avec le hamiltonien
d'un ensemble de plusieurs particules est une constante du mouvement
qui commute avec le hamiltonien ![]() , et il peut y avoir avantage à chercher
les vecteurs propres de
, et il peut y avoir avantage à chercher
les vecteurs propres de ![]() (c'est-à-dire diagonaliser la matrice représentative de
(c'est-à-dire diagonaliser la matrice représentative de
![]() ) dans chacun des sous-espaces
) dans chacun des sous-espaces
![]() associés à un couple de
valeurs propres de
associés à un couple de
valeurs propres de ![]() et de
et de ![]() :
:
Tout ceci revient à dire qu'il y a avantage à choisir pour base de
représentation, les vecteurs propres communs aux observables
![]() et
et ![]() .
.
Cet avantage devient même une nécessité lorsque le système global
considéré possède lui-même un spin déterminé, ![]() par exemple. Sa
désintégration en plusieurs particules, étudiée dans son référentiel
propre, conserve ce spin, et les états finals des divers canaux de
désintégration sont aussi des états de moment angulaire total bien
définiV11 et
égal à
par exemple. Sa
désintégration en plusieurs particules, étudiée dans son référentiel
propre, conserve ce spin, et les états finals des divers canaux de
désintégration sont aussi des états de moment angulaire total bien
définiV11 et
égal à ![]() .
.
Or, nous avons déjà appris à construire ces états
![]() V12 de moment angulaire total
et nous savons déjà que ces états mélangent les états
des particules composantes. Par exemple, la composition de deux
moments angulaires
V12 de moment angulaire total
et nous savons déjà que ces états mélangent les états
des particules composantes. Par exemple, la composition de deux
moments angulaires ![]() et
et ![]() conduit aux états
couplés :
conduit aux états
couplés :
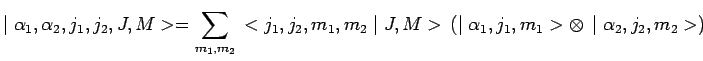 |
avec :
les produits scalaires dans la somme ![]() désignant des
coefficients de Clebsch-Gordan.
désignant des
coefficients de Clebsch-Gordan.
On notera que tous les états de couplage entre moments angulaires, désignent des états dans lesquels les composantes du système total sont inséparables.