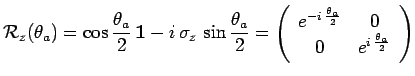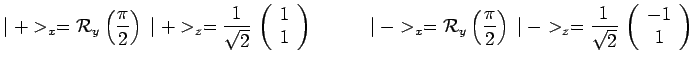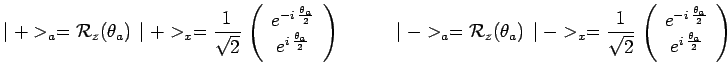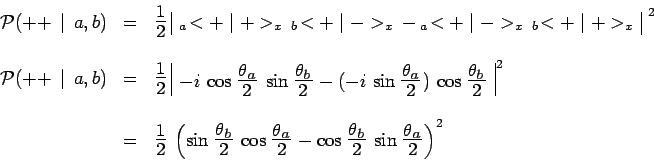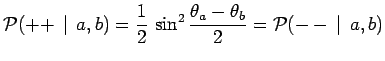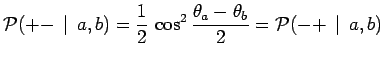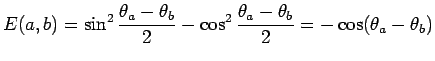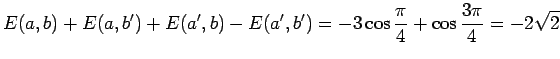


suivant: Le verdict expérimental
monter: Confrontation avec la mécanique
précédent: Confrontation avec la mécanique
Table des matières
On remarque immédiatement que cette probabilité n'est pas en général
factorisableV21, comme il avait été supposé précédemment,
quand on avait écrit :
|
Les probabilités de transition, pour des états à une particule, peuvent
être calculées, en utilisant les opérateurs de rotation :
et donc en particulier :
|
|
On en déduit immédiatement :
d'où résulte finalement :
et en reportant ces résultats partiels dans les expressions des
probabilités :
et en procédant de même pour les autres termes :
et en choisissant les angles :
on obtient finalement :
Le module de cette quantité est supérieure à 2, et l'inégalité de Bell
est donc bien violée.



suivant: Le verdict expérimental
monter: Confrontation avec la mécanique
précédent: Confrontation avec la mécanique
Table des matières
Arnaud Balandras
2005-04-02