Supposons que l'expérience soit d'abord réalisée avec la configuration
![]() , c'est-à-dire que l'on mesure en coïncidence :
, c'est-à-dire que l'on mesure en coïncidence :
La probabilité d'obtenir un événement pour lequel les deux signaux sont
tous deux ![]() ou tous deux
ou tous deux ![]() est la somme des probabilités correspondant aux
cas numéroté 1 et 2 d'une part, et 7 et 8 d'autre part :
est la somme des probabilités correspondant aux
cas numéroté 1 et 2 d'une part, et 7 et 8 d'autre part :
Correspondant aux deux autres configurations on obtient de même :
Or, comme l'indique le tableau, chacune de ces probabilités a
une expressionV39 de
la forme :
et tenu compte de l'état initial dans lequel la paire ![]() est
émise :
est
émise :
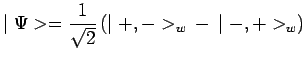 |
![]() désignant une direction queslconque, et par exemple
désignant une direction queslconque, et par exemple ![]() ou
ou ![]() :
:
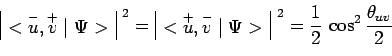 |
![]() désignant l'angle formé entre les deux directions
désignant l'angle formé entre les deux directions ![]() et
et ![]() . Ici
. Ici
![]() d'où :
d'où :
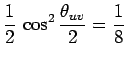 |
Il en résulte immédiatement par exemple :
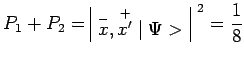 |
et de même :
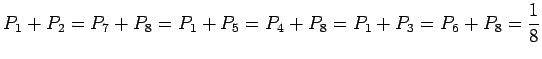 |
ou encore :
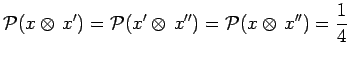 |
Ces dernières équations s'écrivent encore :
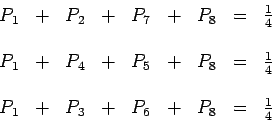 |
d'où en sommant membre à membre :
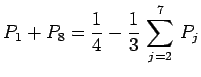 |
Par ailleurs, puisque les huit cas considérés épuisent toutes les
possibilités :
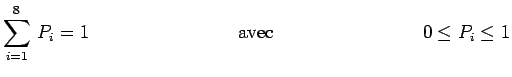 |
d'où :
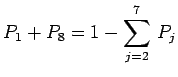 |
En comparant les deux expressions de ![]() on obtient :
on obtient :
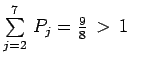 !
!
résultat évidemment aberrant.