b) Remarques

$\imath-$ Il est essentiel de bien remarquer combien ce principe de Born (postulat III) est éminemment paradoxal, non seulement pour le physicien classique, mais aussi tout simplement du point de vue du sens commun. En effet, selon ce principe, les grandeurs qui caractérisent un système physique n'ont pas en général de valeur déterminée. C'est seulement l'observation ou une mesure qui donne une valeur à certaines d'entre elles. Par exemple, à un instant quelconque, une particule n'a pas de position déterminée dans l'espace, on serait tenté de dire qu'elle n'est pas dans l'espace. C'est la mesure qui l'y met, en lui donnant une position plus ou moins précise. Ainsi la réalité du monde, au sens classique, semble avoir perdu sa consistance. Elle est devenue floue et dépendante de l'observation. Pour qui croit en une réalité intrinsèque des objets, la Physique semble avoir perdu son référent, c'est-à-dire ce qui existe indépendamment de l'observateur et qu'elle cherche à décrire. D'une manière générale, il semble en effet que c'est la mesure physique ou plus généralement l'observation qui amène le possible à devenir réel. Le fait est fait et, comme l'avait déjà dit le philosophe grec Protogoras il y a déjà plus de 2500 ans :

$\ll$ L'homme semble bien être alors la mesure de toute chose. $\gg$

et encore bien davantage qu'il ne l'avait pensé. Une telle conclusion parait monstrueuse à certains et explique peut-être pourquoi le mathématicien R. Thom a dit de la mécanique quantique qu'elle constituait le plus grand scandale intellectuel du siècle.

$\imath\imath-$ Dans ce qui précède le ket $\mid \Psi>$ représentatif de l'état quantique du système était supposé normalisé. S'il ne l'est pas alors :

$$\mathcal{P}rob(\hat{A} = a_k)=\mathcal{P}_k= {{\mid <a_k\mid \Psi>\mid ^2}\over{<\Psi\mid \Psi>}}= {{\mid \Psi_k\mid ^2}\over{<\Psi\mid \Psi>}}$$

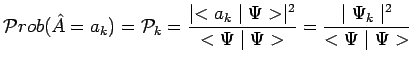Question 2-1 : Vérifier que la somme des probabilités est bien égale à 1 :

$$\sum\limits_{k=1}^\infty~\mathcal{P}_k=1$$

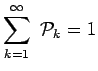$\imath\imath\imath-$ Si la mesure de l'observable $\hat{A}$ est répétée sur un seul système, il est évidemment nécessaire, avant chaque nouvelle mesure, de s'assurer que ce système a bien été remis dans son état initial $\Psi$ .

Plutôt que de répéter $N$ fois ($N\gg 1$ ) la mesure de $\hat{A}$ sur un seul et même système, il est parfois plus facile, comme cela a déjà été dit précédemment, de mesurer $\hat{A}$ en même temps sur $N$ systèmes identiques supposés indépendants et tous placés dans le même état initial $\Psi$ représenté par le ket $\mid \Psi>$ . On admettra que cette deuxième façon de procéder est équivalente à la première, c'est-à-dire fournit les mêmes résultats expérimentaux.

Ainsi, le principe de Born affirme que :

$\imath-$ Tout résultat de mesure de $\hat{A}$ ne peut être que l'une des valeurs propres $a_k$ de $A$ (où $a_k$ est réel puisque $A$ est hermitique).

$\imath\imath-$ Si $N$ désigne le nombre total de mesures effectuées, et si $n_k$ désigne le nombre de fois où la valeur propre $a_k$ a été obtenue, on doit vérifier :

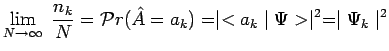$$\lim_{N\to\infty}~{{n_k}\over{N}}=\mathcal{P}r(\hat{A}=a_k)=\mid <a_k\mid \Psi>\mid ^2=\mid \Psi_k\mid ^2$$