Considérons à nouveau l'expérience du cristal de
tourmalineII6 dans laquelle
on mesure, pour chaque photon incident supposé dans un état
![]() , son coefficient de transmission
, son coefficient de transmission ![]() . En raison du
caractère corpusculaire et insécable du photon, cette grandeur
mesurée
. En raison du
caractère corpusculaire et insécable du photon, cette grandeur
mesurée ![]() ne prend que deux valeurs possibles :
ne prend que deux valeurs possibles : ![]() si le
photon est absorbé et
si le
photon est absorbé et ![]() si le photon traverse la lame. On en
déduit que 0
et
si le photon traverse la lame. On en
déduit que 0
et ![]() sont les seules valeurs propres de
l'observable
sont les seules valeurs propres de
l'observable ![]() . Par ailleurs on sait que
. Par ailleurs on sait que ![]() si l'état
incident est polarisé dans la direction de l'axe optique
si l'état
incident est polarisé dans la direction de l'axe optique ![]() et
et
![]() si cet état
si cet état ![]() est polarisé dans la direction
orthogonale
est polarisé dans la direction
orthogonale ![]() :
:
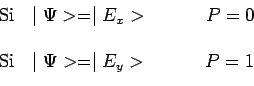 |
On en déduit que ces deux états de polarisation sont des états propres de
![]() correspondant à ces deux valeurs propres :
correspondant à ces deux valeurs propres :
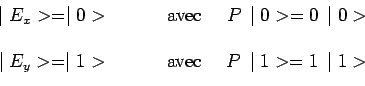 |
On en déduit immédiatement l'expression de l'opérateur unité
![]() et de l'observable
et de l'observable ![]() elle-même, dans l'espace des états de
polarisation du photon :
elle-même, dans l'espace des états de
polarisation du photon :
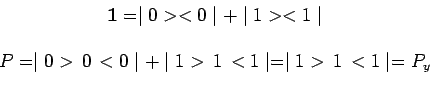 |
L'observable mesurée ![]() est donc simplement le projecteur sur l'état de
polarisation orienté dans la direction
est donc simplement le projecteur sur l'état de
polarisation orienté dans la direction ![]() perpendiculaire à celle de l'axe
optique du cristal.
perpendiculaire à celle de l'axe
optique du cristal.
La décomposition spectrale de l'état initial quelconque de polarisation du
photon :
peut être comparée avec la décomposition classique du champ électrique
incident :
ou encore :
qui laisse pressentir la valeur des produits scalaires :
Conformément au principe de Born, on sait que si le photon incident est dans
un état initial quelconque de polarisation représenté par le ket
Bien évidemment, toutes ces conclusions, fondées sur le formalisme quantique, sont bien conformes aux observations expérimentales :
Par ailleurs, conformément au principe de réduction du paquet
d'ondes, chaque photon qui traverse la lame cristalline en sort
polarisé dans la direction
Si
Si
s'écrit encore, tenu compte des résultats précédents :
On devra donc vérifier expérimentalement :
L'observable
suivant: b) Les deux fentes monter: Illustration des postulats III précédent: Illustration des postulats III Table des matières Arnaud Balandras 2005-04-02 |