L'opérateur ![]() caractérise comment un ensemble de
caractérise comment un ensemble de ![]() systèmes identiques
occupe un ensemble d'états distincts. Il joue un rôle analogue à une fonction
classique de répartition statistique. Une telle fonction s'écrit,
systèmes identiques
occupe un ensemble d'états distincts. Il joue un rôle analogue à une fonction
classique de répartition statistique. Une telle fonction s'écrit, ![]() désignant la constante de Boltzmann :
désignant la constante de Boltzmann :
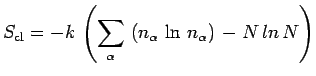 |
où ![]() est le nombre de systèmes dans l'état
est le nombre de systèmes dans l'état ![]() ,
d'où, avec
,
d'où, avec
![]() et
et
![]() :
:
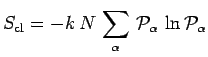 |
Il est donc normal de définir l'entropie ![]() analogue quantique :
analogue quantique :
identique à
![]() sur la base
sur la base
![]() qui diagonalise
qui diagonalise ![]() .
.
On notera, en particulier, que l'entropie d'un cas pur :
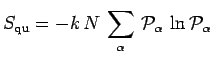 |
est nulle, car chacun des termes de la somme est nul, puisque
![]() ou 0
.
ou 0
.