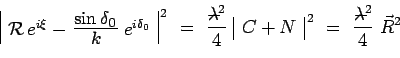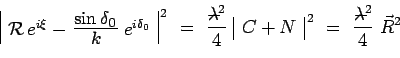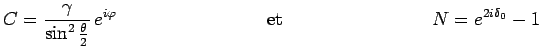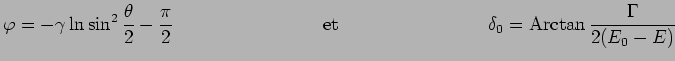|
Pour calculer et représenter la variation de
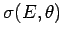 en fonction de
en fonction de 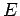 (courbes d'excitation) ou en
fonction de
(courbes d'excitation) ou en
fonction de 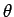 (distributions angulaires) il est commode
d'associer aux nombres complexes
(distributions angulaires) il est commode
d'associer aux nombres complexes 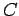 et
et 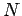 les vecteurs
les vecteurs 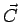 et
et 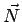 qui les représentent dans le plan complexe
conformément à la figure ci-contre. La variation de
qui les représentent dans le plan complexe
conformément à la figure ci-contre. La variation de 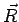 fournit la distribution angulaire quand
fournit la distribution angulaire quand 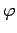 varie en
fonction de
varie en
fonction de 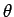 et fournit la courbe d'excitation quand
et fournit la courbe d'excitation quand
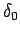 varie en fonction de
varie en fonction de 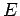 .
.
|
|