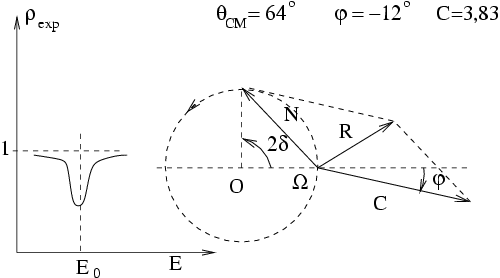
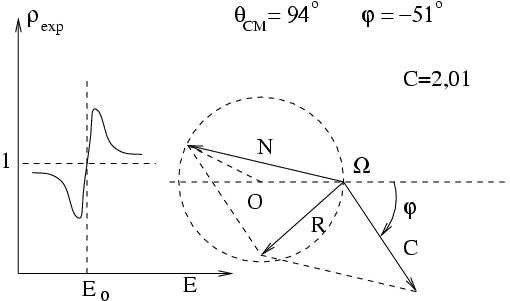
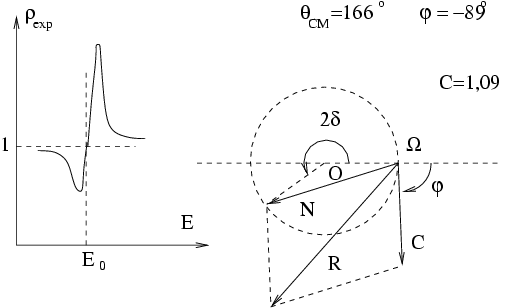
Dans le cas de la diffusion des protons par
![]() , les
courbes d'excitation pour
, les
courbes d'excitation pour
![]() et
et ![]() manifestent l'existence d'une résonance, quand
manifestent l'existence d'une résonance, quand
![]() keV et correspondent à un état excité
de
keV et correspondent à un état excité
de
![]() d'énergie 8289 keV. L'allure expérimentale de
ces trois courbes d'excitation est reproduite au moins
approximativement en utilisant le modèle théorique
précédent et en donnant à ses divers paramètres les
valeurs numériques indiquées ci-après.
d'énergie 8289 keV. L'allure expérimentale de
ces trois courbes d'excitation est reproduite au moins
approximativement en utilisant le modèle théorique
précédent et en donnant à ses divers paramètres les
valeurs numériques indiquées ci-après.
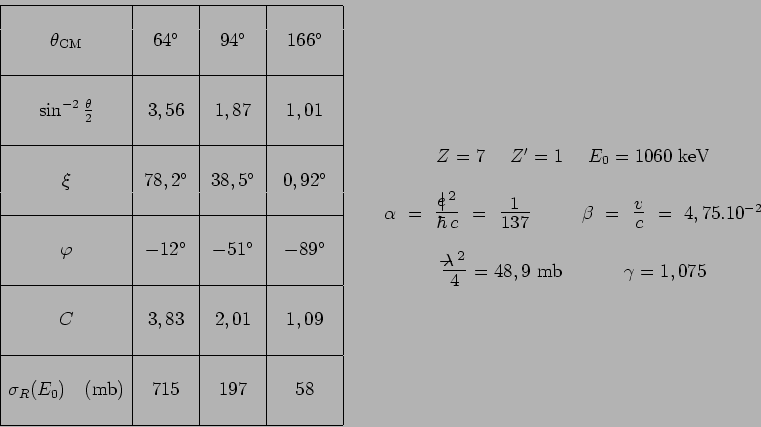 |
Quand ![]() traverse en croissant la valeur
traverse en croissant la valeur ![]() l'angle
l'angle ![]() varie en croissant de 0
à
varie en croissant de 0
à ![]() . Il suffir de reporter sur le
diagramme précédent les valeurs de
. Il suffir de reporter sur le
diagramme précédent les valeurs de ![]() et de
et de ![]() pour en
déduire la variation de
pour en
déduire la variation de ![]() en fonction de l'angle de
déphasage
en fonction de l'angle de
déphasage ![]() . Afin de mieux mettre en évidence l'effet
de la résonance, il est plus significatif de considérer les
variations du rapport suivant :
. Afin de mieux mettre en évidence l'effet
de la résonance, il est plus significatif de considérer les
variations du rapport suivant :
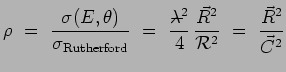 |
On vérifie bien ci-dessous, au moins qualitativement, que le modèle simple théorique rend compte des courbes expérimentales d'excitation :