Remarque :

Tenu compte du fait qu'à l'interface qui sépare l'air et le verre, on doit vérifier :

$$P_r + P_t = 1$$

et en déduire :

$$r^2 + \tau^2 = 1$$

L'application des règles qui viennent d'être rappelées conduit aux résultats qui sont indiqués ci-après en faisant figurer sous chaque processus considéré le produit des amplitudes partielles séquentielles qui lui correspond :

$Z=e^{i\varphi_3}\,r\,e^{i\pi}\,e^{i\varphi_1}$

$Z=e^{i\varphi_5}\,\tau\,e^{i\varphi_3}\,\tau\,e^{i\varphi_1}$

$Z=e^{i\varphi_7}\,\tau\,e^{i\varphi_5}\,r\,e^{i\varphi_3}\,\tau\,e^{i\varphi_1}$

$Z=e^{i\varphi_9}\,\tau\,e^{i\varphi_7}\,r\,e^{i\varphi_5}\,r\,e^{i\varphi_3}\,\tau\,e^{i\varphi_1}$

En faisant ainsi apparaître les diverses réflexions successives qui peuvent concourir à la production du phénomène observé, on obtient les amplitudes totales de réflexion et de transmission :

$$Z_{\mathrm{r\acute{e}flexion}} = e^{i\Phi}\,r\,\left[-1+\tau^2\,e^{2i\bar{\varphi}}+ \tau^2\,r^2\,... ...\bar{\varphi}}+\ldots +\tau^2\,r^{2n}\,e^{i(2n+2)\bar{\varphi}} +\ldots \right]$$

$$Z_\mathrm{transmission} = e^{i(\Phi+\bar{\varphi})}\,\tau^2\,\left[ 1+r^2\,e^{2i\bar{\varphi}}+ \ldots + r^{2n}\,e^{i\,2n\bar{\varphi}} +\ldots \right]$$

$$\mathrm{avec}~~~~~~~~~~\bar{\varphi} = 2\pi\,\frac{e}{\lambda}~~~~~~~~~~\mathrm{et} ~~~~~~~~~~\Phi = \sum_i\,\varphi_i(\mathrm{externe})$$

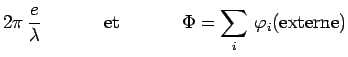Un calcul plus élaboré et fondé sur un meilleur modèle permettrait de vérifier :

$$\mathcal{P}_{\mathrm{r\acute{e}flexion}} + \mathcal{P}_\mathrm{transmission} = \begin{array}{\vert c\vert}Z_{\mathrm{r\acute{e}flexion}}\\ \... ...y}{\vert c\vert}Z_\mathrm{transmission}\\ \end{array}^{\,2} = 1$$

En considérant seulement les deux premiers termes de ces développements et correspondant aux quatre figures ci-dessus, on obtient pour ces deux cas extrêmes :

Si $e=\lambda~~~~~~~~~~\bar{\varphi}=2\pi~~~~~~~~~\mathrm{avec}~~~~~~~~~~\tau=0,98~~~~~~~~r=0,2$

$$Z_r\sim e^{i\Phi}\,r\,(-1+\tau^2)~~~~~~~~~~~~~~~~~~~~~~~~\begin{array}{\vert c\vert}Z_r\\ \end{array}^{\,2} = 0,0016$$

$$Z_t\sim e^{i\Phi}\,\tau\,(1+r^2)~~~~~~~~~~~~~~~~~~~~~~~~\begin{array}{\vert c\vert}Z_t\\ \end{array}^{\,2} = 0,9988$$

Si $e=\frac{\lambda}{2}~~~~~~~~~~\bar{\varphi}=\pi$

$$Z_r\sim -e^{i\Phi}\,r\,(-1-\tau^2)~~~~~~~~~~~~~~~~~~~~~~~~\begin{array}{\vert c\vert}Z_r\\ \end{array}^{\,2} = 0,1537$$

$$Z_t\sim -e^{i\Phi}\,\tau^2\,(1-r^2)~~~~~~~~~~~~~~~~~~~~~~~~\begin{array}{\vert c\vert}Z_t\\ \end{array}^{\,2} = 0,8501$$

et donc :

$\mathcal{P}_{\mathrm{r\acute{e}flexion}} + \mathcal{P}_\mathrm{transmission} \sim 1$

On vérifie ainsi qu'il est bien nécessaire de prendre en compte la totalité de ces développements, ce qui signifie qu'il est nécessaire de considérer toutes les modalités selon lesquelles le phénomène étudié peut se réaliser. Cette observation avait déjà été faite en ce qui concerne les diverses façons selon lesquelles la lumière peut être réfléchie sur un miroir.

La décomposition d'un processus en ses éléments séquenciels peut encore être poursuivie plus finement. En effet, dans toutes les analyses précédentes les périodes ou les étapes successives du processus étaient encore décrites abstraitement. Par exemple la réflexion de la lumière sur un plan ne peut pas, en tant que telle, être considérée comme un mécanisme proprement physique, car la lumière ou le photon : objet physique, ne peut interagir avec un plan géométrique : concept de pensée. La lumière interagit avec la matière et donc seulement avec les atomes qui la constituent.

Par suite, et par exemple, dans le phénomène de réflexion de la lumière (onde ou photon) sur une lame de verre, cette lumière peut interagir avec chacun des atomes de cette lame, et chacun de ces atomes peut d'une certaine manière contribuer à la réalisation du phénomène global observé. Toutefois, il a déjà été expliqué pourquoi en raison d'un mécanisme d'annihilation mutuelle de la plupart des amplitudes, il y avait lieu de ne considérer que les régions de la lame de verre qui sont voisines de la trajectoire classique attribuée au rayon lumineux par le principe de Fermat.

La figure ci-contre indique six couches successives de la lame et espacées d'un intervalle $\varepsilon$ et traversées par une telle trajectoire le long de laquelle la lumière interagit avec un seul atome de chaque couche.   Les rayons incidents correspondant sont décalés de façon à faire apparaître le vecteur amplitude $\vec{Z}_n$ associé à chacun de ces six chemins géométriques, et dont la phase $\varphi_n=\varphi_0-2n\,\bar{\varphi_0}~~$ ( $\bar{\varphi_0}=\frac{2\pi\,\varepsilon}{\lambda}$ ) diminue avec la longueur ou la durée du parcours de ce chemin. Il faut encore multiplier cette amplitude $Z_n$ par celle correspondant à l'interaction de la lumière avec le $n^\mathrm{\grave{e}me}$ atome de la $n^\mathrm{\grave{e}me}$ couche rencontrée sur ce chemin.

Une telle interaction est un phénomène extrêmement complexe qui met en jeu toute la structure de l'atome diffuseur. Le photon incident est absorbé par un des électrons de la couche électronique de cet atome qui échangent eux-mêmes d'autres photons entre eux et avec le noyau. Le photon diffusé peut être alors un nouveau photon réemis par un de ces électrons. Quel que soit la complexité du phénomène, la diffusion du photon incident est affectée d'une amplitude de probabilité qui est simplement un nombre complexe $S=\rho\,e^{i\theta}$ . Il est remarquable que la mécanique quantique permette de schématiser aussi simplement un phénomène aussi complexe.

Néanmoins, le calcul de $S$ est un problème d''electrodynamique quantique qui n'a pas encore été résolu pour un matériau tel que le verre. On sait toutefois :

$$S = \rho\,e^{i\theta}\sim -i\,\rho~~~~~~~~\mathrm{ou}~~~~~~~~\theta\sim -\frac{\pi}{2}~~~~~~~\mathrm{et}~~~~~~~\rho<1$$

Il y a donc lieu de multiplier chacune des amplitudes $Z_i$ par le facteur de réduction $\rho<<1$ et de faire tourner le vecteur $\vec{Z}_i$ d'un angle $-\frac{\pi}{2}$ . Il faut enfin sommer toutes ces amplitudes pour tenir compte de ce que la lumière a été diffusée par l'un quelconque des $n$ atomes considérés. La somme vectorielle des vecteurs $\vec{Z}^\prime_i$ ainsi obtenus et qui représentent les amplitudes $Z^\prime_i = S\,Z_i$ détermine un vecteur résultant $\vec{Z}$ dont le carré du module est égal à la probabilité du processus considéré.

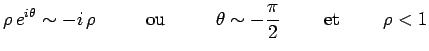On remarque alors que la sommation des amplitudes partielles $\vec{Z}^\prime_i$ engendre une circonférence et que la longueur du vecteur $\vec{Z}$ croît et décroît successivement en fonction du nombre de couches et donc en fonction de l'épaisseur $e$ de la lame de verre, en passant par un maximum dont on sait que le carré est égal à la valeur maximale du coefficient de réflexion soit 0,16. Le rayon $r$ de ce cercle vaut donc 0,2 :

$$(2r)^2 = 0,16$$

On remarque également que le vecteur somme $\vec{Z}$ peut être considéré comme résultant de la somme des deux vecteurs :

$$\vec{Z} = \overrightarrow{AB} ~=~ \overrightarrow{AO} + \overrightarrow{OB} ~=~ -\overrightarrow{Z_A} + \overrightarrow{Z_B}$$

ou encore, en exprimant les amplitudes correspondantes :

$$Z = -r + r\,e^{2i\,\bar{\varphi}}~~~~~~~~~\mathrm{avec}~~~~~~~~~\bar{\varphi} = 2\pi\,\frac{e}{\lambda}$$

$$\mathrm{ou}~~~~~~~~~Z = r\,\left(-1+e^{2i\,\bar{\varphi}}\right)$$

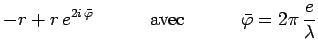On retrouve bien le résultat obtenu précédemment en sommant seulement deux amplitudes : l'une associée à une réflexion sur la face avant et affectée d'un facteur -1, et l'autre associée à une autre réflexion sur la face arrière et affectée seulement d'un facteur de phase correspondant au délai supplémentaire dû à la propagation dans le verre de la lame.

La même analyse peut être faite en ce qui concerne la tranmission de la lumière à travers la lame de verre. Ici encore, on peut ne considérer que les atomes situés le long du chemin optique minimum et l'amplitude est la somme $Z$ des amplitudes $Z_i$ faisant intervenir chacune une seule des couches atomiques successivement traversées par la lumière et auxquelles s'ajoute la plus importante : celle choisie ici pour unité, et correspondant à une transmission directe, sans nécessiter d'interaction intermédiaire avec un atome. On notera que tous les chemins optiques sont identiques et qu'il leur correspond la même phase $\varphi$ :

$$Z = e^{i\,\varphi}\,\left(1+\sum_i\,Z_i\right)$$ De même, les amplitudes $Z_i$ de diffusion par chaque atome sont identiques : $$Z_i = S_i\,\sim\,\rho\,e^{-i\,\frac{\pi}{2}}~=~-i\rho$$ de telle sorte que l'on obtient la construction indiquée ci-contre pour le vecteur amplitude $\vec{Z}$ résultant.

Il faut toutefois remarquer que le lumière diffusée par un atome peut à nouveau être rediffusée par un autre atome et ainsi de suite, avant de sortir de la lame de verre. Ce phénomène s'appelle la diffusion multiple. Quand ce phénomène est pris en compte, le module $$\begin{array}{\vert c\vert}Z\\ \end{array}$$ de l'amplitude totale est bien inférieur à 1 et oscille entre les deux valeurs déjà indiquées 0,92 et 1. Dans ce qui précède, il a toujours été tacitement supposé que le milieu traversé, ici le verre, était parfaitement transparent, c'est-à-dire qu'aucune partie de l'énergie lumineuse n'était perdue entre la source et les récepteurs. Si le milieu est légèrement opaque, l'expression de $S$ en est modifiée, le déphasage est augmenté et le module de $Z$ est diminué.

On notera enfin que le mécanisme de rediffusion des photons par les atomes a pour effet d'introduire un déphasage global $\omega$ du vecteur $\vec{Z}$ . Le sens de ce déphasage correspond à un retard supplémentaire de la lumière qui parvient au récepteur. Tout se passe alors comme si la vitesse de la lumière dans le milieu traversé en avait été diminuée. Ainsi ce ralentissement de la lumière quand elle traverse un milieu matériel correspond à une rotation supplémentaire du vecteur amplitude $\vec{Z}$ , causée par l'interaction des photons avec les atomes du milieu qui réemettent eux-mêmes avec retard (facteur $e^{-i\,\frac{\pi}{2}}$ ) les photons diffusés. C'est donc cette rotation supplémentaire qui explique la valeur de l'indice de réfraction. La physique classique considère que la lumière est constituée d'ondes électro-magnétiques, sous l'effet desquelles les atomes de la matière entrent dans un régime d'oscillations forcées. L'équation différentielle du second ordre qui régit ce mouvement contient un terme de frottement correspondant à l'énergie que cet oscillateur perd en rayonnant. Il en résulte alors mathématiquement que cette énergie est rayonnée avec le même retard que celui obtenu précédemment.

Ces dernières remarques visent à montrer comment un même phénomène physique peut être expliqué de différentes manières. Ces différentes manières ne sont toutefois pas équiva-lentes car leur portée explicative, c'est-à-dire l'étendue du domaine expérimental dans lequel elles demeurent pertinentes, peut être très inégale. Notamment dans tout ce qui précède, aucune des propriétés éventuelles d'anisotropie de la lumière et de la matière n'a été prise en compte. Or, les propriétés de polarisation de la lumière ou des photons, ainsi que les propriétés directionnelles de la structure cristalline de la matière peuvent jouer un rôle essentiel et modifier considérablement les phénomènes observés.