D) Factorisation des amplitudes

Précédemment, chaque amplitude de probabilité était associée et relative à un processus complet, c'est-à-dire reliant un état initial (I) résultant d'une préparation expérimentale à un état final (F) donnant lieu à une observation effective. Une étude plus approfondie d'un tel processus conduit souvent à le décomposer en une séquence de processus plus élémentaires : $\alpha,\ldots,\gamma,\ldots$ et nous savons déjà que l'amplitude de probabilité correspondant à cette séquence est égale au produit des amplitudes partielles :

$$I - \alpha,\beta,\ldots,\gamma - F = <F\mid\gamma><\gamma\ldots\alpha><\alpha\mid I>$$

Lorsque les étapes intermédiaires ne sont pas effectivement observées, mais constituent seulement un catalogue d'éventualités, on sait déjà également qu'il y a lieu de sommer sur toutes ces possibilités avant d'élever le module au carré :

$$\mathcal{P}rob~(I\to F) = \begin{array}{\vert c\vert}\sum\limits_{\alpha\ldots\gamma}\,... ...id\gamma><\gamma\ldots\alpha><\alpha\mid I>\\ \end{array}^{\,2}$$

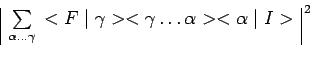pour obtenir l'expression de la probabilité du processus complet. Ce sont ces règles qui vont être illustrées ci-après, en analysant les expériences précédentes de réflexion et de transmission de la lumière monochromatique par une lame de verre.

Dans le cadre du modèle très simple utilisé précédemment, les amplitudes partielles associées aux processus élémentaires sont résumées dans le tableau suivant :

Processus élémentaire	Amplitude $Z$
Propagation dans l'air ou le verre	$e^{i\varphi}$
Réflexion de l'air dans l'air	$r\,e^{i\pi}$
Réflexion du verre dans le verre	$r$
Transmission de l'air dans le verre	$\tau$
ou du verre dans l'air

et dans le cas des incidences normales seulement considérées ici : $r=0,2$ et $\tau=0,98$

$$\varphi = 2\pi\,\frac{\Delta t}{\tau} ~=~ 2\pi~\frac{\ell}{\lambda}$$

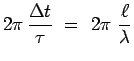$\ell$ désignant la longueur du trajet parcouru.