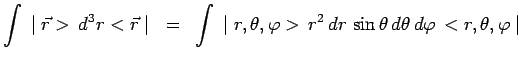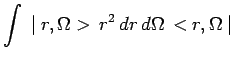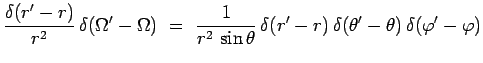


suivant: Remarque :
monter: Moments cinétiques et harmoniques
précédent: Moments cinétiques et harmoniques
Table des matières
| |
Choisir une représentation de Schrödinger c'est choisir pour base
les vecteurs propres d'un E.C.O.C. construit avec les observables
de position. Dans le cas d'un système constitué d'une seule
particule de spin nul, ces observables peuvent être les
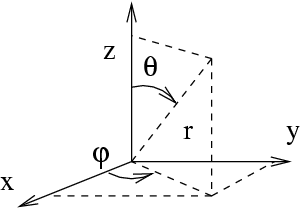
coordonnées cartésiennes 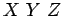 ou les coordonnées
sphériques
ou les coordonnées
sphériques
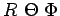 . Bien entendu, ces deux groupes
d'observables sont liées entre eux par des relations qui
définissent des fonctions d'observables images des relations
classiques :
. Bien entendu, ces deux groupes
d'observables sont liées entre eux par des relations qui
définissent des fonctions d'observables images des relations
classiques :
|
|
et les vecteurs propres de ces deux E.C.O.C. se
correspondent de telle sorte que si :
et avec :
alors :
et pour un vecteur ket 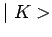 quelconque :
quelconque :
Le changement de variables peut être effectué à l'aide de la
relation de fermeture :
que l'on peut écrire symboliquement :
Les relations correspondantes d'orthonormalisation s'en
déduisent :



suivant: Remarque :
monter: Moments cinétiques et harmoniques
précédent: Moments cinétiques et harmoniques
Table des matières
Arnaud Balandras
2005-04-02