Dans un atome, chaque électron est soumis à une attraction
centrale, issue du noyau, et à ses interactions avec les autres
électrons. Du fait de la symétrie approximativement
sphérique de l'atome, on peut montrer qu'à titre
d'approximation ces interactions ont pour effet de corriger
l'attraction du noyau, sans toutefois détruire son caractère
central. Il résulte de cette approximation que chacun des
électrons se meut indépendamment des autres, comme si il
était seul et plongé dans un potentiel central
avec une énergie potentielle ![]() qui tient compte de la présence
de tous les autres électrons et néanmoins qui ne dépend
que de la distance au centre de l'atome.
qui tient compte de la présence
de tous les autres électrons et néanmoins qui ne dépend
que de la distance au centre de l'atome.
Un tel système, quand il est constitué d'un seul électron,
admet donc pour hamiltonien :
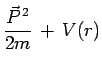 |
![]() désignant l'observable vectorielle
impulsion. Dès lors, l'hamiltonien est une observable scalaire,
invariante par rotation, et qui commute donc avec les
générateurs de ces rotations dans l'espace :
désignant l'observable vectorielle
impulsion. Dès lors, l'hamiltonien est une observable scalaire,
invariante par rotation, et qui commute donc avec les
générateurs de ces rotations dans l'espace :
| 0 |
En particulier, ![]() commute avec
commute avec
![]() et
et ![]() et nous
allons donc chercher à déterminer les vecteurs propres communs
à cet E.C.O.C.
et nous
allons donc chercher à déterminer les vecteurs propres communs
à cet E.C.O.C.
Question 3-30 : Expliquez d'abord physiquement et ensuite mathématiquement pourquoi :
![]() Quand
Quand ![]() alors
alors
![]()
![]() Quand
Quand ![]() alors
alors
![]() et
et
![]()