De cette définition dérive immédiatement tout
un ensemble de propriétés très importantes. Si ![]() désigne un opérateur
linéaire quelconque :
désigne un opérateur
linéaire quelconque :
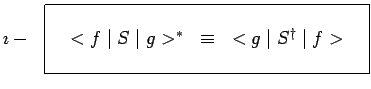 |
De même
![]()
et puisque ![]() et
et ![]() sont quelconques :
sont quelconques :
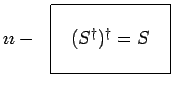 |
On peut également écrire :
d'où, puisque ![]() et
et ![]() sont quelconques :
sont quelconques :
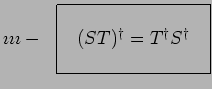 |
Question 1-4 : Soit trois opérateurs hermitiques quelconques A,B et C. Démontrez que les opérateurs P et Q suivants sont également hermitiques :
Question 1-5 : A désignant un opérateur hermitique, m un
entier positif et ![]() un vecteur ket quelconque, démontrez
:
un vecteur ket quelconque, démontrez
: