Si
![]()
![]() régulière
à l'infini a un pôle d'ordre
régulière
à l'infini a un pôle d'ordre ![]() à l'origine. Il n'existe
donc pas dans ce cas de solution physique d'énergie négative.
à l'origine. Il n'existe
donc pas dans ce cas de solution physique d'énergie négative.
Si
![]()
![]() est une solution régulière
partout à laquelle correspond les solutions physiques :
est une solution régulière
partout à laquelle correspond les solutions physiques :
Une telle fonction d'onde décrit une particule d'énergie
cinétique
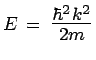 et de moment
angulaire
et de moment
angulaire ![]() .
.
L'ensemble de ces fonctions propres de ![]() constitue une base
complète sur laquelle il est intéressant de développer une
onde plane.
constitue une base
complète sur laquelle il est intéressant de développer une
onde plane.
L'onde plane
![]() est également une
fonction propre de
est également une
fonction propre de ![]() correspondant à une particule d'énergie
correspondant à une particule d'énergie
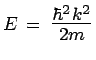 et d'impulsion
et d'impulsion
![]() . Cette fonction d'onde peut être
développée sur la base des états précédents, soit :
. Cette fonction d'onde peut être
développée sur la base des états précédents, soit :
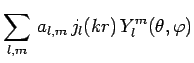 |
et on démontre :
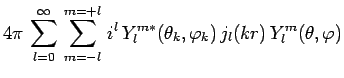 |
ou plus simplement en choisissant l'axe ![]() dans la
direction de
dans la
direction de ![]() :
:
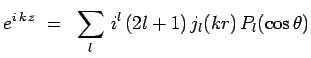 |
![]() désignant le polynôme de Legendre
d'ordre
désignant le polynôme de Legendre
d'ordre ![]() , à savoir :
, à savoir :
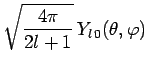 |