![]()
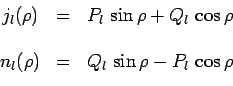 |
![]() est un polynôme en
est un polynôme en
![]() d'ordre
d'ordre
![]() et de parité
et de parité
![]()
![]() est un polynôme en
est un polynôme en
![]() d'ordre
d'ordre ![]() et de parité
et de parité ![]()
soit par exemple :
 |
 |
![]() Si
Si
![]() :
:
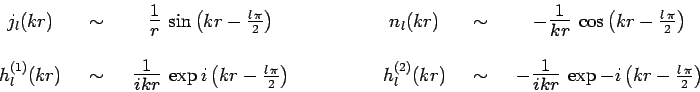 |
Ces approximations sont valables dès lors que :
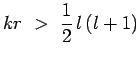 |
![]() Si
Si ![]() :
:
![]() comme
comme ![]()
![]() ont un pôle d'ordre
ont un pôle d'ordre ![]()
Si
![]() soit
soit
![]() . Il
faut remplacer
. Il
faut remplacer ![]() par
par ![]() et la seule solution bornée à
l'infini est :
et la seule solution bornée à
l'infini est :
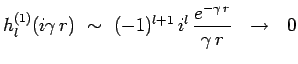 |