Lorsque ![]() prend sa valeur maximale
prend sa valeur maximale
![]() la
fonction d'onde devient plus simple et on obtient alors :
la
fonction d'onde devient plus simple et on obtient alors :
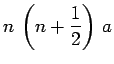 |
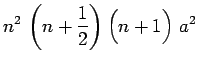 |
On en déduit l'expression de l'écart quadratique radial :
![$\displaystyle \left[ <r^2> - <r>^2\right]^{\frac{1}{2}} ~=~
\frac{<r>}{\sqrt{2n+1}}$](img2630.png) |
Ainsi, lorsque ![]() devient très grand, l'électron reste
pratiquement localisé dans une coquille sphérique de rayon
devient très grand, l'électron reste
pratiquement localisé dans une coquille sphérique de rayon
![]() et dont l'épaisseur, de l'ordre de
et dont l'épaisseur, de l'ordre de ![]() , est
très faible. Par ailleurs, l'énergie du niveau excité
, est
très faible. Par ailleurs, l'énergie du niveau excité
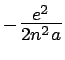 est la même que celle d'un
électron classique décrivant une orbite circulaire de rayon
est la même que celle d'un
électron classique décrivant une orbite circulaire de rayon
![]() . Sur cet exemple particulier, on retrouve bien les lois du
mouvement classique lorsque les nombres quantiques prennent des
valeurs élevéesIII22. Tout se
passe comme si l'électron parcourait des orbites circulaires de
rayon
. Sur cet exemple particulier, on retrouve bien les lois du
mouvement classique lorsque les nombres quantiques prennent des
valeurs élevéesIII22. Tout se
passe comme si l'électron parcourait des orbites circulaires de
rayon ![]() .
.