Il est intéressant d'indiquer les premières fonctions propres de l'atome d'hydrogène.
Pour ![]() , on obtient la fonction d'onde de l'état
fondamental :
, on obtient la fonction d'onde de l'état
fondamental :
Cette fonction est indépendante de ![]() et
et ![]() et
représente donc un état qui possède la symétrie
sphérique. D'une façon plus générale, les états
et
représente donc un état qui possède la symétrie
sphérique. D'une façon plus générale, les états ![]() pour lesquels
pour lesquels ![]() ne dépendent pas des variables
angulaires et sont sphériques. On obtient ainsi pour les états
ne dépendent pas des variables
angulaires et sont sphériques. On obtient ainsi pour les états
![]() avec
avec ![]() et
et ![]() :
:
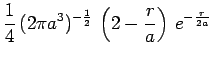 |
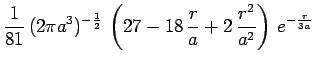 |
On remarquera que la probabilité de trouver l'électron dans
une coquille sphérique de rayon ![]() et d'épaisseur
et d'épaisseur ![]() est
donnée par l'expression :
est
donnée par l'expression :
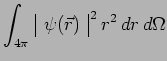 |
Dans le cas où
![]() il vient :
il vient :
|
|
Il est intéressant de connaître la valeur moyenne de ![]() et de
et de
![]() dans l'état quantique représenté par la fonction
d'onde
dans l'état quantique représenté par la fonction
d'onde
![]() :
:
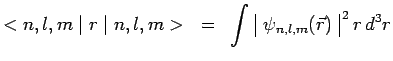 |
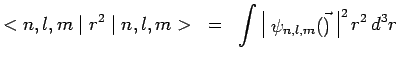 |
On trouve ainsi notamment :
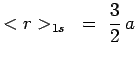 |
![$\displaystyle \frac{1}{2}\,a\,[3n^2 - l\,(l+1)]$](img2620.png) |
le paramètre ![]() ayant été défini ci-dessus :
ayant été défini ci-dessus :
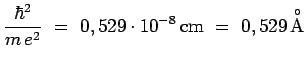 |
On notera soigneusement l'ordre de grandeur (
![]() cm) des dimensions de l'atome d'hydrogène dans ses premiers
états. On remarquera que l'électron est d'autant plus
éloigné en moyenne du proton que
cm) des dimensions de l'atome d'hydrogène dans ses premiers
états. On remarquera que l'électron est d'autant plus
éloigné en moyenne du proton que ![]() est grand.
est grand.