Considérons un système physique dont on sait qu'il se trouve dans
l'un de ![]() états possibles
états possibles ![]() avec une
probabilité
avec une
probabilité
![]() . A cette situation est associé
comme nous l'avons déjà vuIV2 un
opérateur densité :
. A cette situation est associé
comme nous l'avons déjà vuIV2 un
opérateur densité :
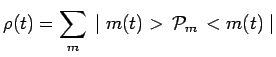 |
Cherchons à quelle équation du mouvement satisfait
l'opérateur ![]() . A cet effet, il y a lieu de remarquer que
les nombres
. A cet effet, il y a lieu de remarquer que
les nombres
![]() sont constants au cours du temps, car
aussi longtemps qu'il n'est pas l'objet d'une mesure
expérimentale, le système ne peut changer d'état d'évolution et
passer d'un état d'évolution
sont constants au cours du temps, car
aussi longtemps qu'il n'est pas l'objet d'une mesure
expérimentale, le système ne peut changer d'état d'évolution et
passer d'un état d'évolution
![]() à un autre état
à un autre état
![]() . Par ailleurs, les évolutions des kets et des bras
sont régies par les équations conjuguées :
. Par ailleurs, les évolutions des kets et des bras
sont régies par les équations conjuguées :
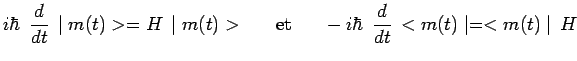 |
de telle sorte que :
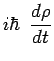 |
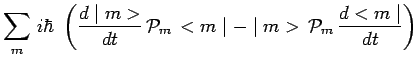 |
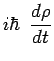 |
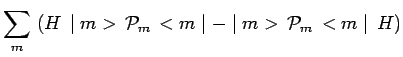 |
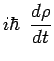 |
![\begin{displaymath}\begin{array}{\vert ccc\vert}
\hline
& & ~ \\
~ & i\hbar\,\s...
...er{dt\strut}$} = -[\rho,H] & ~ \\
& & ~ \\
\hline
\end{array}\end{displaymath}](img2764.png) |
Ainsi l'opérateur densité évolue, tout comme les états, d'une façon parfaitement détermi-niste, et se trouve déterminé à chaque instant à partir de son expression initiale. Il est intéressant de noter l'analogie formelle entre l'équation précédente et l'équation classique qui régit l'évolution temporelle dans l'espace des phases et qui sera rappelée ci-après.
Pour déterminer la dépendance temporelle de l'opérateur densité
quantique ![]() , il n'est pas nécessaire d'intégrer l'équation
précédente. Il suffit de se reporter à sa définition :
, il n'est pas nécessaire d'intégrer l'équation
précédente. Il suffit de se reporter à sa définition :
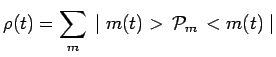 |
et d'utiliser l'opérateur unitaire d'évolution temporelle des
états :
d'où il résulte immédiatement :
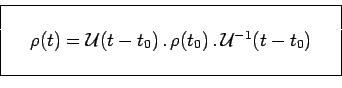 |
La trace d'un produit de matrices est invariante dans une permutation circulaire
de ses facteurs, et il en résulte :
Si l'état initial du système physique étudié est un cas pur :
d'où cette conséquence importante :
|