suivant monter précédent table des matières
suivant: b) Interprétation monter: La quatrième relation d'indétermination précédent: La quatrième relation d'indétermination   Table des matières

a) Démonstration

Soit un système $ \cal S$ , une quelconque $ A$ de ses observables et son hamiltonien $ H$ . Comme pour tout autre couple d'observables, elles satisfont une inégalité de Heisenberg :

$\displaystyle \Delta A_\Psi.\Delta H_\Psi\geq \frac{1}{2}\,\mid \left<\,\left[A,H\right]\,\right>_\Psi\mid$      

Par ailleurs, l'observable $ A$ satisfait une équation d'Ehrenfest qui s'écrit, si $ A$ comme nous le supposons ne dépend pas du temps :

$\displaystyle i\hbar\frac{d}{dt}\left<A\right>_\Psi=\left<\,\left[A,H\right]\,\right>_\Psi$      

de telle sorte que, en rassemblant les deux résultats précédents :

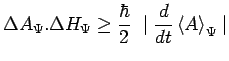$\displaystyle \Delta A_\Psi.\Delta H_\Psi\geq \frac{\hbar}{2}~\mid \frac{d}{dt}\left<A\right>_\Psi\mid$      

ou encore :

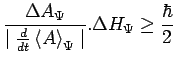$\displaystyle \frac{\Delta A_\Psi}{\mid \frac{d}{dt}\left<A\right>_\Psi\mid }. \Delta H_\Psi\geq\frac{\hbar}{2}$      

Nous allons maintenant définir une durée de vie, encore appelée vie moyenne de l'état $ \Psi$ .

Bien évidemment, on ne peut dire qu'un système a changé d'état, que lorsqu'un tel changement est expérimentalement observable :

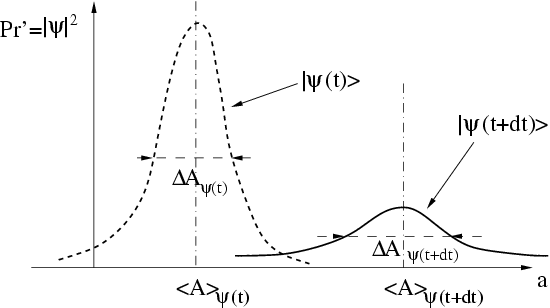
\epsffile{/home/arnaud/DossierLambert/DossierLambert/Figures/evolution.eps}

Classiquement cela signifie que une ou plusieurs des observables ont changé de valeur. En mécanique quantique, une telle définition du changement d'état est sans signification, puisqu'en général, même dans un état bien déterminé, aucune de ces observables n'a de valeur définie. Seule la valeur moyenne de chaque observable est bien définie. Il y aura donc changement d'état lorsque la valeur moyenne de l'une au moins des observables du système aura varié d'une quantité appréciable. Pour cela, il faut que cette variation, obtenue au bout d'un temps $ \Delta t$ , soit comparable ou supérieure à la dispersion des valeurs de cette observable $ A$ dans l'état initial $ \Psi$ du système, ce qui revient à écrire :

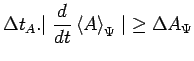$\displaystyle \Delta t_A.{\mid \frac{d}{dt}\left<A\right>_\Psi\mid }\geq\Delta A_\Psi$      

puisque l'écart-type $ \Delta A_\Psi$ mesure précisément cette dispersion de l'état $ \Psi$ . On remarque que $ \Delta t_A$ dépend de l'observable $ A$ considérée, et mesure sa vitesse significative d'évolution temporelle. Des deux relations précédentes, on déduit alors :

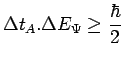$\displaystyle \Delta t_A.\Delta E_\Psi\geq\frac{\hbar}{2}$      

en notant $ \Delta E_\Psi=\Delta H_\Psi$ la dispersion en énergie de l'état physique considéré. Si enfin, on définit la vie moyenne $ \Delta t_\Psi$ d'un état comme la borne supérieure des $ \Delta t_A$ quelle que soit l'observable $ A$ :

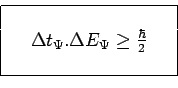\begin{displaymath}\begin{array}{\vert ccc\vert} \hline & & \\ ~ & \Delta t_\Ps... ...ta E_\Psi\geq\frac{\hbar}{2} & ~ \\ & & \\ \hline \end{array}\end{displaymath}      

Cette inégalité constitue la quatrième inégalité de Heisenberg.

suivant monter précédent table des matières
suivant: b) Interprétation monter: La quatrième relation d'indétermination précédent: La quatrième relation d'indétermination   Table des matières
Arnaud Balandras 2005-04-02