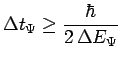 |
Cette inégalité indique que la dispersion en énergie de l'état d'un système fixe
une borne inférieure à sa durée de vie moyenne :
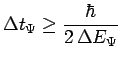 |
Notamment, si le système est dans un de ses états propres d'énergie,
![]() est nul, et la durée de vie
est nul, et la durée de vie
![]() est infinie. C'est
le cas des solutions particulières de l'équation de Schrödinger, qui ont
été appelées des solutions stationnaires.
est infinie. C'est
le cas des solutions particulières de l'équation de Schrödinger, qui ont
été appelées des solutions stationnaires.
La précédente inégalité présente une grande analogie formelle avec les
autres inégalités de Heisenberg telles que :
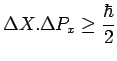 |
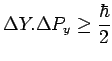 |
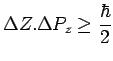 |
Toutefois, il y a lieu de rappeler ici que ces trois inégalités font toutes
intervenir des écarts-types d'observables, tandis que
![]() n'est
pas un tel écart-type, puisque selon la mécanique quantique non relativiste, le temps
n'est
pas un tel écart-type, puisque selon la mécanique quantique non relativiste, le temps ![]() n'est pas représenté par une observable quantique.
n'est pas représenté par une observable quantique.
Cependant, on peut remarquer que la durée de vie d'un état
peut être une grandeur mesurable aléatoire. Il en est ainsi
par exemple, de la durée de vie d'un état excité atomique,
puisque l'instant ![]() de sa désintégration est imprévisible.
Dès lors,
de sa désintégration est imprévisible.
Dès lors, ![]() mesure l'indétermination de la date
mesure l'indétermination de la date ![]() de cet événement. D'une manière analogue, nous avons
déjà remarquéIV9 que la
dispersion en impulsion, et donc également en énergie
de cet événement. D'une manière analogue, nous avons
déjà remarquéIV9 que la
dispersion en impulsion, et donc également en énergie ![]() ,
d'un paquet d'ondes est liée à l'indétermination
,
d'un paquet d'ondes est liée à l'indétermination ![]() qui frappe l'instant
qui frappe l'instant ![]() de passage du centre
de passage du centre ![]() de ce paquet
d'ondes en un point
de ce paquet
d'ondes en un point ![]() d'observation, par la même relation :
d'observation, par la même relation :
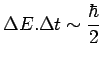 |
tandis que la localisation éventuelle ![]() de la particule au
voisinage de
de la particule au
voisinage de ![]() est elle-même frappée des indéterminations
est elle-même frappée des indéterminations
![]() et
et ![]() . Dès lors, et dans ce cas, les quatre inégalités
précédentes de Heisenberg peuvent être rassemblées en une seule qui est
:
. Dès lors, et dans ce cas, les quatre inégalités
précédentes de Heisenberg peuvent être rassemblées en une seule qui est
:
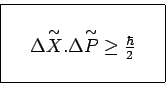 |
![]() désignant les quatre
indéterminations qui affectent les coordonnées du 4-vecteur
événe-ment : détection de la particule au point
désignant les quatre
indéterminations qui affectent les coordonnées du 4-vecteur
événe-ment : détection de la particule au point ![]() à l'instant
à l'instant ![]() , et par ailleurs
, et par ailleurs
![]() désignant les quatre indéterminations qui affectent les
coordonnées
désignant les quatre indéterminations qui affectent les
coordonnées
![]() et
et ![]() du 4-vecteur impul-sion-énergie de
cette particule.
du 4-vecteur impul-sion-énergie de
cette particule.