d) Dégénérescence

Si il existe plusieurs vecteurs propres $\mid a,x>$ linéairement indépendants associés à la même valeur propre $a$ , cette valeur propre est dite dégénérée.

L'indice $x$ , qui permet de repérer les différents vecteurs propres distincts $\mid a,x>$ associés à la même valeur propre $a$ :

$A\mid a,x>=a\mid a,x>$

peut prendre des valeurs discrètes :

$x=1,2,3,\ldots,n,\ldots$

et la dégérescence est dite alors d'ordre $n$ , ou toutes les valeurs d'un intervalle :

$-\infty<\alpha\leq x\leq\beta<+\infty$

qui peut être infini.

Les vecteurs propres $\mid a,x>$ avec $a$ fixé, associés à une même valeur propre $a$ , engendrent un sous-espace vectoriel $\cal{H}_{\cal{S}}$ ($a$ ) de $\cal{H}_{\cal{S}}$ tel que :

$\forall \mid f>\in~$ $\cal{H}_{\cal{S}}$ ($a$ ) $~~\Longrightarrow~~A\mid f>=a\mid f>$

En effet, si $~\mid f>=\sum\limits_i f_i \mid a,i>~~\left( \mathrm{ou}~~=\int_\alpha^\beta f(x)\mid a,x>dx~\right)$

$A\mid f>=\sum\limits_i ~f_i~ A\mid a,i>~~\left( \mathrm{ou}~~=\int_\alpha^\beta ~f(x)~A\mid a,x>dx~\right)~=~a\mid f>$

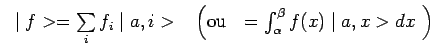
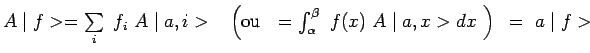
Ainsi, à chacune des valeurs propres $a$ de $A$ est associé un sous-espace $\cal{H}_{\cal{S}}$ ($a$ ) dont $tous$ les vecteurs sont vecteurs propres de $A$ avec la même valeur propre $a$ .

Bien évidemment un vecteur propre $\mid a>$ associé à une valeur propre $a$ de $A$ est également défini à un facteur $\lambda$ près $(\lambda\in{\cal{C}})$ que, dans la suite, nous supposerons choisi de telle sorte que le vecteur propre $\mid a>$ soit normé, soit au sens de Kronecker :

$<a_i\mid a_j>=\delta_{ij}~~~~~$ (spectre discret)

soit au sens de Dirac :

$<a\mid a^\prime>=\delta(a-a^\prime)~~~~~$ (spectre continu)

On postulera que deux vecteurs propres associés, l'un à une valeur propre dépendant d'un spectre discret, l'autre à une valeur propre dépendant d'un spectre continu sont toujours orthogonaux, à savoir :

$<a_i\mid a>=<a\mid a_i>=0$