|
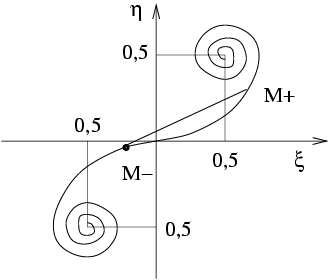
Le lieu du point géométrique
quand |
Plutôt que de calculer les intégrales de Fresnel, il est commode d'utiliser la construction graphique suivante :
|
|
Cette courbe est telle que ![]() est précisément l'abscisse
curviligne, mesurée à partir de l'origine
est précisément l'abscisse
curviligne, mesurée à partir de l'origine ![]() , du point
, du point ![]() et que la tangente en ce point fait avec l'axe des
et que la tangente en ce point fait avec l'axe des ![]() un angle
égal à
un angle
égal à
![]() .
.
L'intensité de la tache de diffraction au point ![]() a
pour valeur :
a
pour valeur :
Pour évaluer comment varie
![]() en fonction de
en fonction de
![]() , il suffit donc d'examiner comment varie la
longueur du segment
, il suffit donc d'examiner comment varie la
longueur du segment
![]() en fonction de
en fonction de
![]() en remarquant que la longueur
en remarquant que la longueur ![]() de l'arc
de l'arc ![]() :
:
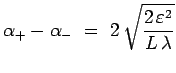 |
est elle-même constante. Cette dernière
remarque permet également de voir comment varie la structure et
notamment les contrastes des raies sombres et claires de la tache
de diffraction en fonction des paramètres ![]() ,
,
![]() et
et ![]() .
.