|
|
La source |
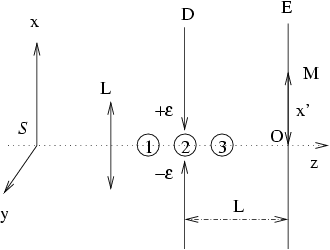
On utilise le dispositif expérimental schématisé sur la figure suivante et semblable à celui déjà considéré dans une question précédenteIV18.
|
|
![]() désignant par exemple un
paquet d'ondes à une dimension semblable à ceux déjà
considérés précédemmentIV19 :
désignant par exemple un
paquet d'ondes à une dimension semblable à ceux déjà
considérés précédemmentIV19 :
 |
La traversée de la fente carrée de largeur
![]() provoque la réduction des paquets d'ondes
provoque la réduction des paquets d'ondes
![]() et
et
![]() de telle
sorte que :
de telle
sorte que :
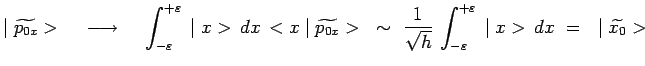 |
en faisant l'approximation :
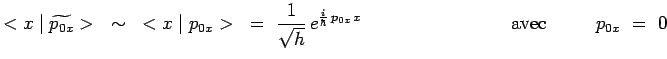 |
d'où résulte finalement, en renormalisant :
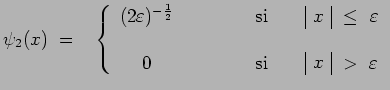 |
Immédiatement à la sortie de la fente, la fonction d'onde de
la particule est donc celle d'une particule approximativement bien
localisée :
![]() et
et
![]() :
:
 |
Il reste à étudier l'évolution temporelle de cet état.
Chacun de ces trois facteurs évolue indépendamment des deux
autres puisque l'hamiltonien est celui d'une particule libre, et
que les composantes de l'impulsion sont des observables qui
commutent :
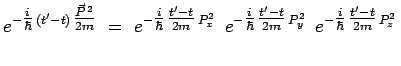 |
Le troisième facteur
![]() est donc
simplement multiplié par un facteur de phase. Par contre les
deux autres évoluent de manière identique et cette évolution
temporelle peut être décrite, avec
est donc
simplement multiplié par un facteur de phase. Par contre les
deux autres évoluent de manière identique et cette évolution
temporelle peut être décrite, avec ![]() , en utilisant le
propagateur
, en utilisant le
propagateur ![]() qui vient d'être défini :
qui vient d'être défini :
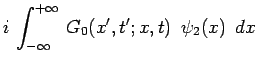 |
soit encore explicitement :
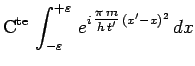 |
La particule tombe sur l'écran ![]() à un instant
à un instant
![]() et par suite :
et par suite :
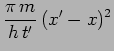 |
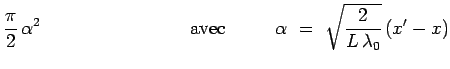 |
![]() désignant la longueur d'onde associée
à la particule incidente :
désignant la longueur d'onde associée
à la particule incidente :
La distribution des points d'impact qui construisent la figure de
diffraction est régie par la fonction d'onde :
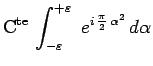 |
soit encore, en introduisant les intégrales de Fresnel
:
 |
avec :
et :
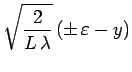 |
L'intensité
![]() de la tache au point
de la tache au point ![]() d'ordonnée
d'ordonnée
![]() mesure la probabilité de détection de la particule
en ce point :
mesure la probabilité de détection de la particule
en ce point :
On retrouve le résultat classique qui rendait bien compte de la structure macroscopique de la tache de diffraction obtenue avec une source lumineuse. Par contre, la physique classique, qui ne fait intervenir que la structure ondulatoire de la lumière, ne peut expliquer la structure fine microscopique, constitués de multiples points d'impact localisés et bien séparés. Seule la mécanique quantique peut expliquer la coexistence de ces deux aspects : corpusculaire au niveau microscopique et ondulatoire au niveau macroscopique.