Conformément au principe de BornIV34la probabilité de transition de l'état initial I à l'un
quelconques des états finals
![]() a pour
expression :
a pour
expression :
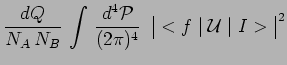 |
![]() et
et ![]() désignant respectivement le nombre de
projectiles et le nombre de cibles mis en jeu dans l'expérience.
désignant respectivement le nombre de
projectiles et le nombre de cibles mis en jeu dans l'expérience.
Il suffit maintenant de rassembler les résultats partiels,
déjà obtenus précédemment, en les introduisant dans la
formule précédente :
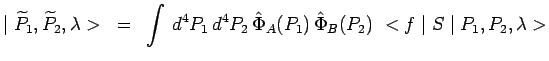 |
avec :
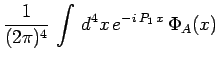 |
et avec :
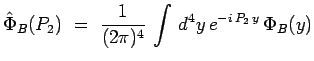 |
et :
Le ![]() de Dirac rend immédiate l'intégration sur
de Dirac rend immédiate l'intégration sur
![]() et impose la valeur
et impose la valeur
![]() . Si, par
ailleurs, dans
. Si, par
ailleurs, dans
![]() on fait l'approximation
d'assimiler les variables
on fait l'approximation
d'assimiler les variables ![]() et
et ![]() qui figurent dans
qui figurent dans ![]() à leurs valeurs moyennes
à leurs valeurs moyennes
![]() et
et
![]() , l'intégration sur
, l'intégration sur ![]() fournit un
fournit un
![]() qui rend à son tour immédiate l'intégration
sur
qui rend à son tour immédiate l'intégration
sur ![]() , de telle sorte qu'il reste :
, de telle sorte qu'il reste :
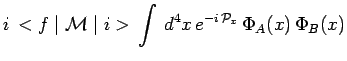 |
L'intégration qui suit sur
![]() fournit un
fournit un
![]() rendant immédiate l'intégration sur
rendant immédiate l'intégration sur ![]() et
on obtient enfin :
et
on obtient enfin :
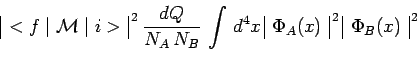 |
Le second membre de cette équation est le produit de trois facteurs :
|
Bien évidemment, il ne peut y avoir réaction entre ![]() et
et ![]() et transition vers un nouvel état final que si un projectile
et transition vers un nouvel état final que si un projectile ![]() et une cible
et une cible ![]() se trouvent en même temps au même endroit.
se trouvent en même temps au même endroit.