Normalisations

suivant: d) Expression théorique de monter: Schéma d'une expérience de précédent: c) Probabilités de transition Table des matières

Normalisations

Pour comparer l'expression théorique qui vient d'être obtenue avec celle qui définit la section efficace expérimentale, il faut établir une relation entre la normalisation des fonctions d'onde $\Phi_A$ et $\Phi_B$ d'une part et les densités expérimentales $\rho_A$ et $\rho_B$ d'autre part.

A cet effet, on rappelle :

$\displaystyle \mid\widetilde{P},\lambda>$

$\displaystyle =$

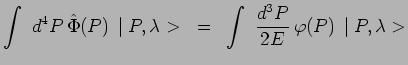$\displaystyle \int~d^4P\,\hat{\Phi}(P)\,\mid P,\lambda> ~=~ \int~\frac{d^3P}{2E}\,\varphi(P)\,\mid P,\lambda>$

et on peut alors égaler deux expressions du nombre de particules :

$\displaystyle <\widetilde{P},\lambda\mid\widetilde{P},\lambda>$

$\displaystyle =$

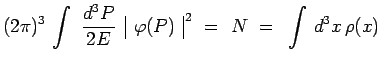$\displaystyle (2\pi)^3\,\int~\frac{d^3P}{2E}\,~\begin{array}{\vert c\vert}\varphi(P)\\ \end{array}^{\,2} ~=~ N ~=~ \int\,d^3x\,\rho(x)$

On rappelle également la définition de $\Phi(x)$ :

$\displaystyle \Phi(x)$

$\displaystyle =$

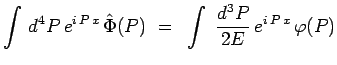$\displaystyle \int\,d^4P\,e^{i\,P\,x}\,\hat{\Phi}(P) ~=~ \int~\frac{d^3P}{2E}\,e^{i\,P\,x}\,\varphi(P)$

et il en résulte :

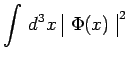$\displaystyle \int\,d^3x~\begin{array}{\vert c\vert}\Phi(x)\\ \end{array}^{\,2}$

$\displaystyle =$

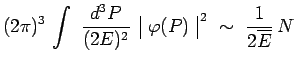$\displaystyle (2\pi)^3\,\int~\frac{d^3P}{(2E)^2}\,~\begin{array}{\vert c\vert}\varphi(P)\\ \end{array}^{\,2}~\sim~\frac{1}{2\overline{E}}\,N$

en admettant que le facteur $(2E)^{-1}$ varie peu dans l'intervalle d'intégration où $\varphi(P)\,\not=\,0$ et en l'assimilant à sa valeur moyenne. On obtient donc finalement :

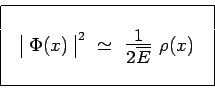$\begin{displaymath}\begin{array}{\vert c\vert}\hline { }\\ ~~\begin{array}{\vert... ...\frac{1}{2\overline{E}}$}~\rho(x) ~~\\ { }\\ \hline \end{array}\end{displaymath}$

suivant: d) Expression théorique de monter: Schéma d'une expérience de précédent: c) Probabilités de transition Table des matières

Arnaud Balandras 2005-04-02