a) Spectre non dégénéré

Si l'observable

constitue à elle seule en E.C.O.C., ce qui implique qu'aucune de ses valeurs propres ne soit dégénérée, et si son spectre est entièrement discret, ce qui implique que ses valeurs propres sont indiçables :

et constituent un ensemble dénombrable, tout ket $\mid f>$ est décomposable, d'une façon unique, sur la base $\{\mid a_i>\}$ de telle sorte que :

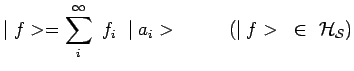$\displaystyle \mid f>=\sum\limits_i^\infty~f_i~\mid a_i>~~~~~~~~(\mid f>~\in~{\cal{H}_{\cal{S}}})$

$<a_i\mid a_j>=\delta_{ij}~~~$ d'où $~~~<a_j\mid f>=f_j$

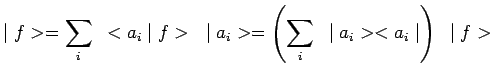$\displaystyle \mid f>=\sum\limits_i~<a_i\mid f>~\mid a_i>=\left(\sum\limits_i~\mid a_i><a_i\mid \right)~\mid f>$

$\begin{displaymath}\begin{array}{\vert c\vert} \hline { } \\ ~~~\mathrm{Si} <a_... ...{i=1}^\infty~\mid a_i><a_i\mid~~~ \\ { } \\ \hline \end{array}\end{displaymath}$

Cette expression de l'opérateur unité, sous forme d'une somme de projecteurs, s'appelle une décomposition spectrale de l'opérateur unité et s'appelle également relation de fermeture.

Cette décomposition fait en effet intervenir le spectre complet des valeurs propres de

et l'ensemble complet de ses vecteurs propres $\mid a_i>$ . On notera que cette décomposition de l'opérateur unité est une conséquence directe des relations d'orthonormalisation de la base.

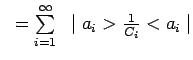
Si $<a_i\mid a_j>~=~C_i\delta_{ij}~~~~$ alors 1 $~=\sum\limits_{i=1}^\infty~\mid a_i>{{1}\over{C_i}}<a_i\mid$

La décomposition spectrale de l'opérateur unité sur la base $\{\mid a_i>\}$ permet d'obtenir immédiatement une transposition numérique de toutes les relations algébriques formelles :

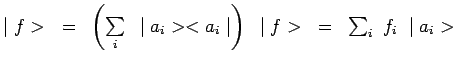
Si $<a_i\mid a_j>=\delta_{ij}~~~$ alors $\mid f>=~$ 1 $\mid f>~=~\left(\sum\limits_{i}~\mid a_i><a_i\mid \right)~ \mid f>~=~\sum_i~f_i~\mid a_i>$

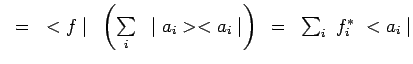
$<f\mid ~=~<f\mid$ 1 $~=~<f\mid ~\left(\sum\limits_{i}~\mid a_i><a_i\mid \right)~ =~\sum_i~f_i^*~<a_i\mid$

avec $f_i=<a_i~\mid f>$ et $f_i^*=<f\mid a_i>$ . Le ket $\mid f>$ a pour composantes les nombres

, et son bra conjugué $<f\mid$ les composantes

imaginaires conjuguées des

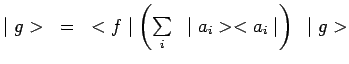
$<f\mid g>~=~<f\mid$ 1 $\mid g>~=~ <f\mid \left(\sum\limits_{i}~\mid a_i><a_i\mid \right)~\mid g>$

$<f\mid g>~=~\sum\limits_i~<f\mid a_i><a_i\mid g>~=~\sum\limits_i~f_i^*~g_i$

$<f\mid g>~=~\sum\limits_i~f_i^*~g_i$

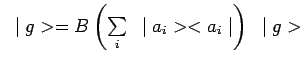
$\mid f>=B$ 1 $~\mid g>= B\left(\sum\limits_{i}~\mid a_i><a_i\mid \right)~\mid g>$

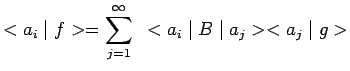$\displaystyle <a_i\mid f>=\sum\limits_{j=1}^{\infty}~<a_i\mid B\mid a_j><a_j\mid g>$

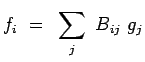$B_{ij}=<a_i\mid B\mid a_j>$ désignant les éléments d'une matrice

représentative de l'opérateur

sur la base orthonormée $\{\mid a_i>\}$ .

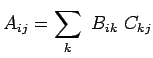$\displaystyle A_{ij}=\sum\limits_k~B_{ik}~C_{kj}$

$\displaystyle <a_i\mid H\mid a_j>=<a_i\mid H^\dagger\mid a_j>=<a_j\mid H\mid a_i>^*$

Ainsi sur une base orthonormée, un opérateur hermitique est représenté par une matrice hermitique.

Sur la base $\{\mid a_i>\}$ constituée de ses vecteurs propres, l'observable

est représentée par une matrice diagonale :

$\displaystyle <a_i\mid A\mid a_j>=a_i~\delta_{ij}~~~~~~~A_{ij}=a_i~\delta_{ij}$

On notera qu'en général, le nombre des composantes

des vecteurs kets et vecteurs bras est infini, et que les matrices $(B_{ik})$ représentatives des opérateurs

ont un nombre infini de lignes et de colonnes.

Question 1-15 : Démontrez que si deux observables A et B commutent, l'une quelconque d'entre elles, A par exemple, n'a d'éléments de matrice non nuls qu'entre des vecteurs propres de l'autre, B, relatifs à la même valeur propre, soit, par exemple :

$(b-b^\prime)<b,x\mid A\mid b^\prime,x^\prime>=0$

a) Spectre non dégénéré - discret