Si le spectre des valeurs propres de l'observable ![]() est non
dégénéré mais continu, l'ensemble des vecteurs propres
est non
dégénéré mais continu, l'ensemble des vecteurs propres ![]() forme encore une base, mais non dénombrable. Si
forme encore une base, mais non dénombrable. Si ![]() désigne le ou les intervalles qui contiennent ces valeurs
propres (réelles puisque
désigne le ou les intervalles qui contiennent ces valeurs
propres (réelles puisque ![]() est hermitique) on écrira, pour
tout vecteur
est hermitique) on écrira, pour
tout vecteur ![]() de
de
![]() :
:
 |
Cette expression de ![]() s'appelle encore la décomposition
spectrale du vecteur
s'appelle encore la décomposition
spectrale du vecteur ![]() . Nous supposerons toujours, dans ce
cas, que la base est orthonormée à la manière de Dirac, c'est-à-dire
:
. Nous supposerons toujours, dans ce
cas, que la base est orthonormée à la manière de Dirac, c'est-à-dire
:
de telle sorte que, quel que soit
![]() :
:
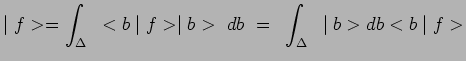 |
Si
![]() alors
1
alors
1
![]()
On obtient ainsi une autre décomposition spectrale de l'opérateur unité, et également une autre expression de la relation de fermeture.
Sur une telle base
![]() tout ket
tout ket ![]() est repéré
par une infinité non dénombrable de composantes
est repéré
par une infinité non dénombrable de composantes ![]()
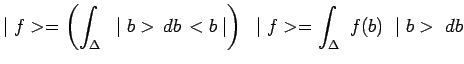 |
avec :
L'ensemble des composantes ![]() constitue une fonction, en
général complexe, de la variable réelle
constitue une fonction, en
général complexe, de la variable réelle ![]() . Cette fonction
s'appelle la fonction d'onde représentative du ket
. Cette fonction
s'appelle la fonction d'onde représentative du ket ![]() .
.
Le vecteur bra conjugué ![]() du vecteur ket
du vecteur ket ![]() sera
défini par la fonction d'onde complexe conjuguée :
sera
défini par la fonction d'onde complexe conjuguée :
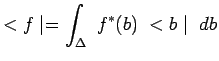 |
de telle sorte que le produit scalaire prend la forme :
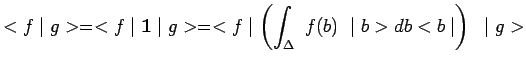 |
|||
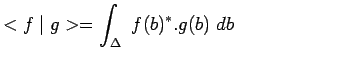 |