Une base est alors constituée de tous les vecteurs propres de
![]() les uns
les uns ![]() associés aux valeurs propres discrètes
associés aux valeurs propres discrètes
![]() et les autres
et les autres ![]() associés aux valeurs propres
associés aux valeurs propres ![]() du spectre continu. Ces vecteurs de base sont orthonormalisés
comme suit :
du spectre continu. Ces vecteurs de base sont orthonormalisés
comme suit :
et l'expression de l'opérateur unité en résulte :
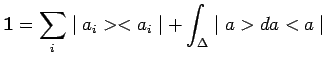 |
On pourra écrire symboliquement :
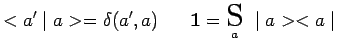 |
![]() désignant un delta de Kronecker ou un delta de
Dirac, ou même 0
, selon que
désignant un delta de Kronecker ou un delta de
Dirac, ou même 0
, selon que ![]() et/ou
et/ou ![]() appartiennent à un
spectre discret ou continu.
appartiennent à un
spectre discret ou continu.