Remarque

Le produit scalaire $<f\mid g>$ aurait pu être également calculé à partir des deux expressions :

$$<f\mid =\int_\Delta~f^*(b^\prime)<b^\prime\mid db^\prime~~~~~~~~~\mathrm{et}~~~~~~~~~~~\mid g>= \int_\Delta~g(b)\mid b>db$$

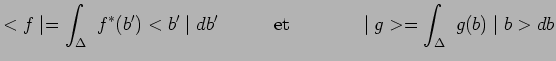de telle sorte que :

$$<f\mid g>=\int_\Delta~db.g(b)\int_\Delta~db^\prime~f^*(b^\prime)<b^\prime\mid b>$$

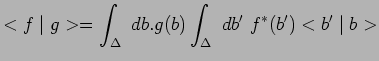Or en vertu d'un théorème fondamental :

$$<b^\prime\mid b>=0~~~~~~~~~~~\mathrm{si}~~~~~~~~~~~b^\prime\not=b$$

$Si$ donc le produit scalaire $<b^\prime\mid b>$ des deux vecteurs de base était $une$ $fonction$ des deux variables continues $b$ et $b^\prime$ , cette fonction, en tant que fonction de $b^\prime$ dépendant du paramètre $b$ , serait nulle partout, sauf pour $b^\prime=b$ , c'est-à-dire nulle presque partout (au sens des mathématiques : sauf sur un ensemble de mesure nulle). Or l'intégrale d'une $fonction$ nulle presque partout est identiquement nulle. Cette intégrale sur la variable $b^\prime$ étant nulle, il en résulterait que le produit scalaire :

$$<f\mid g>=0$$

quel que soit $\mid f>$ et $\mid g>$ . Tous les états seraient orthogonaux entre eux, ce qui est incompatible avec la décomposition spectrale initiale des vecteurs kets $\mid f>$ et $\mid g>$ .

Pour éviter une conséquence aussi catastrophique, Dirac postula que le produit scalaire $<b^\prime\mid b>$ n'était pas une fonction, mais un nouvel être mathématique qui fût appelé ensuite une distribution, dont la signification purement opérationnelle sous un signe d'intégration a déjà été donnée :

$$<b^\prime\mid b>=\delta(b-b^\prime)~~~~~~~~~\mathrm{et}~~~~~~~~~ \int_\Delta~db^\prime~f^*(b^\prime)\delta(b-b^\prime)=f^*(b)$$

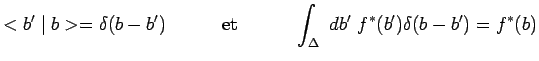et on retrouve bien pour $<f\mid g>$ le résultat précédent qui avait été obtenu lui-même en postulant la décomposition spectrale de l'opérateur unité.

Question 1-16 : On démontre d'ailleurs aisément que les relations d'orthonormalisation et de fermeture s'entrainent mutuellement :

$$<a^\prime\mid a>=\delta(a^\prime-a)~~~\Longleftrightarrow~~~ \mathbf{1}=\int_\Delta \mid a>da<a\mid$$

Sur une telle base $\{\mid a>\}$ tout opérateur $A$ sera représenté par une fonction ou une distribution dépendant de deux variables continues. Par exemple :

$$\mathrm{Si}~~~\mid f>=A\mid g>~~~\mathrm{on~d\acute{e}duit}$$

$$<a\mid f>=<a\mid A\mathbf{1}\mid g>=<a\mid A\left(\int\mid a^\prime> da^\prime<a\mid \right)~\mid g>$$

$$\mathrm{Soit}~~~f(a)=\int A(a,a^\prime)~g(a^\prime)~da^\prime$$

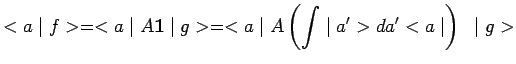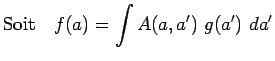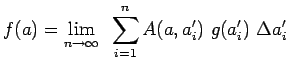dont on notera la correspondance avec la définition habituelle de l'intégrale comme limite d'une somme $\sum$ :

$$f(a)=\lim\limits_{n\rightarrow\infty}~\sum\limits_{i=1}^n A(a,a_i^\prime)~g(a_i^\prime)~\Delta a_i^\prime$$