Soit le vecteur propre
on en déduit, par
application répétée de 
, une suite de 
vecteurs
, tous vecteurs propres de 
avec la même
valeur propre
et en même temps vecteurs propres
de 
avec les valeurs propres 
avec
soit :
 |
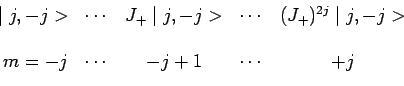Tout opérateur fonction des composantes de 
et appliqué à un
élément de cette suite engendre un vecteur dépendant de cette même suite.
Les vecteurs de cette suite forment la base non normalisée d'un espace à
dimensions.
On en déduit une base orthonormée en procédant comme suit.
Soit
les vecteurs de cette base orthonormée :
 |
et soit :
 |
Calculons la norme de
d'où l'on déduit la
valeur de 
:
 |
|||
![$\displaystyle =[j(j+1)-m(m+1)]<j,m\mid j,m>\hbar^2$](img625.png){kind=small} |
et donc :
![$\displaystyle \mid C_m\mid ^2=\left[j(j+1)-m(m+1)\right]~\hbar^2$](img626.png){kind=small} |
La constante
est donc définie à un facteur de phase
près. Par convention on choisit
réel et positif. Il en résulte :
Soit 
un ensemble d'observables qu'il faut adjoindre à
et
pour constituer un E.C.O.C. et désignons
par 
les valeurs propres de
. Soit
un ensemble de vecteurs propres communs à
,
et
,
constitué d'un ensemble de suites
dont chacune est
associée à une valeur propre
et a été construite
selon la méthode précédente. Un tel ensemble s'appelle une
base standard. Sur une telle base, les opérateurs de
moment angulaire admettent des représentations matricielles
standards :
Si, par exemple
, on trouve avec :
 |
 |
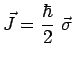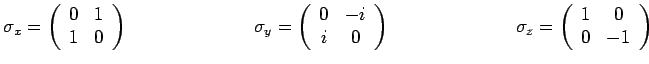Ces trois matrices s'appellent les matrices de Pauli.
Question 1-21 : Dans le cas où 
écrivez
explicitement les matrices représentatives des opérateurs
et des observables
en classant
les vecteurs de base
dans l'ordre des valeurs de 
décroissantes.