f) Valeurs propres

Puisque $\vec{J}^2$ et $J_z$ constituent un E.C.O.C. leurs vecteurs propres communs constituent une base que nous allons déterminer. Soit $\xi~\hbar^2$ une valeur propre de $\vec{J}^2$ :

$$\vec{J}^2~\mid \xi>~=~\xi~\hbar^2~\mid \xi>$$

d'où :

$$<\xi\mid \vec{J}^2\mid \xi>=\sum\limits_{i=1}^3~<\xi\mid J_i.J_i\mid \xi>=\xi~\hbar^2<\xi\mid \xi>$$

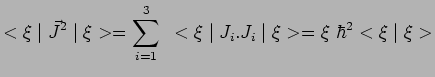Puisque les normes des vecteurs $\mid \xi>$ et $J_i\mid \xi>$ sont positives ou nulles, on en déduit :

$$\xi~\geq~0$$

et on pose $\xi=j(j+1)$ avec $j\geq 0$ ou $j\leq -1$ . Si $j\leq -1$ il suffit de poser $\mathcal{J}=-j-1$ d'où $\mathcal{J}\geq 0$ pour se ramener au cas général :

$$j~\geq~0$$

Le système complet des vecteurs propres communs aux observables $\vec{J}^2$ et $J_z$ est donc constitué des vecteurs $\mid j,m>$ tels que :

$$\vec{J}^2\mid j,m>=j(j+1)\hbar^2~\mid j,m>$$

$$J_z\mid j,m>=m\hbar~\mid j,m>$$

Compte tenu des relations antérieures :

$$<j,m\mid J_-J_+\mid j,m>=[j(j+1)-m(m+1)]\,\hbar^2\,<j,m\mid j,m>$$

$$<j,m\mid J_+J_-\mid j,m>=[j(j+1)-m(m-1)]\,\hbar^2\,<j,m\mid j,m>$$

et puisque les normes des vecteurs sont toutes positives :

$$m(m+1)-j(j+1)\leq 0$$

$$m(m-1)-j(j+1)\leq 0$$

Pour chacun de ces deux trinomes négatifs ou nuls, la valeur de $m$ doit être comprise entre celles des deux racines :

$$-j-1\leq m \leq j$$

$$-j\leq m \leq j+1$$

et donc finalement :

$$\begin{array}{\vert c\vert}\hline { }\\ ~~-j\leq m \leq +j~~\\ { }\\ \hline \end{array}$$

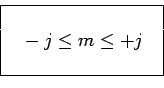Les relations précédentes impliquent :

Si $~~~m=j~~~~~~J_+\mid j,j>=0$

$~~~~~~~m=-j~~~~~J_-\mid j,-j>=0$

Or, par ailleurs :

$\vec{J}^2J_+\mid j,m>=J_+\vec{J}^2\mid j,m>=j(j+1)\hbar^2~J_+\mid j,m>$

$J_z J_+\mid j,m>=(J_+J_z+\hbar J_+)\mid j,m>=(m+1)\hbar~J_+\mid j,m>$

et de même avec $J_-$ :

$\vec{J}^2J_-\mid j,m>=J_-\vec{J}^2\mid j,m>=j(j+1)\hbar^2~J_-\mid j,m>$

$J_z J_-\mid j,m>=(J_-J_z-\hbar J_-)\mid j,m>=(m-1)\hbar~J_-\mid j,m>$

Ainsi à partir d'un vecteur propre $\mid j,m>$ , on peut déduire la suite des vecteurs et des valeurs propres suivants :

$$\begin{array}{ccccc} (J_-)^p \mid j,m> & \cdots & \mid j,m> &... ...p)\hbar & \cdots & m\hbar & \cdots & (m+q)\hbar \\ \end{array}$$

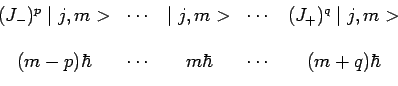Pour que les bornes imposées précédemment aux valeurs de $m$ ne puissent être franchies, il est donc nécessaire qu'il existe des valeurs $p$ et $q$ telles que :

$$J_+\mid j,q>=0~~~~~~~~~~~~~~~~~~~~~~~~J_-\mid j,p>=0$$

Les éventualités précédemment envisagées sont donc nécessairement réalisées :

$J_+\mid j,j>=0~~~~~\mathrm{et~donc}~~~~~q=j~~~~~~~~~J_-\mid j,-j>=0 ~~~\mathrm{et~donc}~~~p=-j$

Par ailleurs, $N$ et $N^\prime$ désignant des entiers positifs ou nuls :

$m=m_{max}-N=j-N$

$m=m_{min}+N^\prime=-j+N^\prime$

et donc :

$2m=N^\prime-N=$ entier $\gtrless 0$

$2j=N^\prime+N=$ entier $\geq 0$

En conclusion $2j$ est un entier positif ou nul, et $2m$ est un entier positif, négatif ou nul tel que :

$$-j\leq m\leq+j$$