c) Caractéristique du cas pur

Il est alors évident, avec $<\Psi\mid \Psi>=1$ et $\rho=\mid \Psi><\Psi\mid$ :

$$\rho^2=\rho$$

Inversement, supposons que $\rho^2=\rho$ avec $\mathrm{Tr}~\rho=1$ .

La base $\mid \varphi_i>$ qui diagonalise $\rho$ diagonalise également $\rho^2$ et sur cette base :

$$\rho^2=\rho~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{entraine}~~~~~~~~~~~~~~~~~~~~~~~~ \rho^2_{ii}=\rho_{ii}=\mathcal{P}_i=\mathcal{P}_i^2$$

Ces valeurs propres $\mathcal{P}_i$ sont donc nulles ou égales à 1 et de l'équation :

$$\mathrm{Tr}\,\rho=\sum\limits_i\,\mathcal{P}_{ii}=1$$

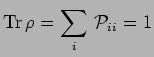résulte qu'une seule de ces valeurs propres $\mathcal{P}_i$ est égal à 1 de telle sorte que :

$$\rho=\sum\limits_i\,\mid \varphi_i>\,\mathcal{P}_i\,<\varphi_i\mid =\mid \varphi><\varphi\mid$$

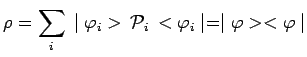La condition nécessaire et suffisante pour que la matrice $\rho$ soit celle d'un cas pur s'écrit donc :

$\rho^2=\rho$