Dans le mode de représentation adopté jusqu'à maintenant et
appelé le mode de représen-tation de Schrödinger, noté
![]() dans la suite, chaque état
dans la suite, chaque état ![]() d'évolution du
système physique
d'évolution du
système physique ![]() étudié est codé ou représenté dans
étudié est codé ou représenté dans
![]() par des vecteurs kets
par des vecteurs kets
![]() et dans
et dans
![]() par des
vecteurs bras imaginaires conjugués
par des
vecteurs bras imaginaires conjugués
![]() et
fonction du temps. Par contre toute grandeur physique
et
fonction du temps. Par contre toute grandeur physique ![]() bien
définie et indépendante du temps est codée ou
représentée par un opérateur, une observable
bien
définie et indépendante du temps est codée ou
représentée par un opérateur, une observable ![]() , dont la
forme est elle-même bien déterminée, invariable et
indépendante du temps. Il en résulte que les vecteurs propres
, dont la
forme est elle-même bien déterminée, invariable et
indépendante du temps. Il en résulte que les vecteurs propres
![]() ou
ou ![]() d'une observable sont eux-mêmes
indépendants du temps. Dans la décomposition spectrale du
vecteur ket
d'une observable sont eux-mêmes
indépendants du temps. Dans la décomposition spectrale du
vecteur ket
![]() sur la base constituée des états
propres de l'observable
sur la base constituée des états
propres de l'observable ![]() :
:
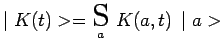 |
ce sont les coefficients ![]() qui dépendent du temps et qui
paramétrisent l'évolution temporelle du système.
qui dépendent du temps et qui
paramétrisent l'évolution temporelle du système.
Nous allons maintenant décrire le système dans
![]() à partir
d'un repère mobile par rapport au repère précédent
du mode de représentation
à partir
d'un repère mobile par rapport au repère précédent
du mode de représentation
![]() . Ce repère
mobile se déplacera conformément à la loi d'évolution du
système
. Ce repère
mobile se déplacera conformément à la loi d'évolution du
système ![]() étudié dont les états d'évolution paraîtront
alors invariables. Au contraire, l'ensemble des états et donc des
vecteurs kets qui précédem-ment étaient fixes, vont être
animés d'un mouvement général d'évolution, inverse de
celui appliqué au repère mobile, de telle sorte que, du fait
de cette transformation :
étudié dont les états d'évolution paraîtront
alors invariables. Au contraire, l'ensemble des états et donc des
vecteurs kets qui précédem-ment étaient fixes, vont être
animés d'un mouvement général d'évolution, inverse de
celui appliqué au repère mobile, de telle sorte que, du fait
de cette transformation :
Ainsi tout vecteur ket ![]() fixe dans
fixe dans
![]() devient un vecteur ket
devient un vecteur ket
![]() dépendant du temps dans ce
nouveau mode de représentation, appelé le mode de
représentation de Heisenberg, et noté
dépendant du temps dans ce
nouveau mode de représentation, appelé le mode de
représentation de Heisenberg, et noté
![]() .
.
Toutefois, si
![]() désigne un état d'évolution du
système :
désigne un état d'évolution du
système :
sa traduction dans
![]() devient bien, comme cela avait
été annoncé, un vecteur fixe :
devient bien, comme cela avait
été annoncé, un vecteur fixe :
Par ailleurs, la transformation définie par l'opérateur
![]() est une transformation unitaire du type
de celles étudiées précédemmentIV12.
Les considérations qui ont alors éte développées
précisent les lois de transformation simultanée des vecteurs,
des opérateurs et des observables :
est une transformation unitaire du type
de celles étudiées précédemmentIV12.
Les considérations qui ont alors éte développées
précisent les lois de transformation simultanée des vecteurs,
des opérateurs et des observables :
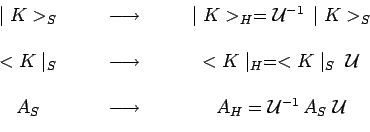 |
Ainsi, tout opérateur ![]() indépendant du temps dans
indépendant du temps dans
![]() , du
fait que l'expression classique
, du
fait que l'expression classique ![]() de la grandeur physique considérée ne
dépend pas elle-même du temps, devient dans
de la grandeur physique considérée ne
dépend pas elle-même du temps, devient dans
![]() un opérateur
un opérateur
![]() dont l'expression même dépend du temps.
dont l'expression même dépend du temps.
Dès lors, les équations d'évolution ne vont plus porter sur les vecteurs
représentatifs des états, qui sont constants, mais sur les observables
telles que ![]() .
.
De l'expression de ![]() en fonction de
en fonction de ![]() on déduit :
on déduit :
et en dérivant par rapport au temps :
![$\displaystyle \left[\,\frac{d}{dt}\,\mathcal{U}(t)\,\right]\,A_H(t)+
\mathcal{U}(t)\,\frac{dA_H}{dt}=
A_S\,\left[\,\frac{d}{dt}\,\mathcal{U}(t)\,\right]$](img2928.png) |
et, en utilisant l'équation d'évolution :
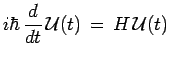 |
on obtient successivement :
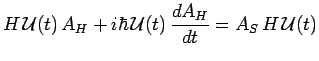 |
et, en multipliant à gauche par
![]() :
:
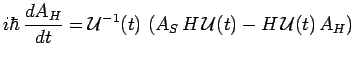 |
mais :
de telle sorte que :
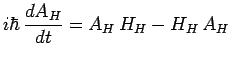 |
d'où finalement les équations d'évolution auxquelles satisfont
toutes les observables dans
![]() :
:
![\begin{displaymath}\begin{array}{\vert ccc\vert}
\hline
& & \\
~ & i\hbar\,\fra...
...t}\,A_H=\left[A_H,H_H\right] & ~ \\
& & \\
\hline
\end{array}\end{displaymath}](img2935.png) |
Ces équations s'appellent les équations de Heisenberg.
Question 4-9 : Si l'expression classique de la variable dynamique
![]() dépend du temps,
dépend du temps,
![]() , et donc est représentée
dans
, et donc est représentée
dans
![]() par une observable
par une observable ![]() dépendant du temps,
démontrez que dans
dépendant du temps,
démontrez que dans
![]() cette observable satisfait l'équation de
Heisenberg :
cette observable satisfait l'équation de
Heisenberg :
![$\displaystyle i\hbar\,\frac{d}{dt}\,A_H=\left[A_H,H_H\right]+i\hbar\,\frac{\partial}{\partial t}\,A_H$](img2938.png) |
en notant par convention :
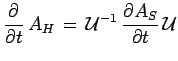 |
De la décomposition spectrale d'un vecteur ket
![]() écrite dans
écrite dans
![]() et représentative d'un état
d'évolution :
et représentative d'un état
d'évolution :
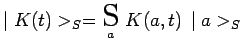 |
on déduit immédiatement son expression dans
![]() en
appliquant l'opérateur
en
appliquant l'opérateur
![]() aux deux membres de cette équation
:
aux deux membres de cette équation
:
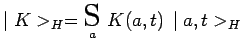 |
On remarque que les coefficients ![]() qui mesurent les probabilités sont
bien invariants, comme ils doivent l'être en raison de leur signification physique
:
qui mesurent les probabilités sont
bien invariants, comme ils doivent l'être en raison de leur signification physique
: