Fonction d'observables

De nombreuses grandeurs physiques classiques sont définies par référence à d'autres grandeurs plus fondamentales. C'est ainsi que dans le formalisme classique de Hamilton toutes les variables dynamiques sont fonctions de variables de positions $q_1,...,q_i,...$ et de moments canoniquement conjugués qui sont des sortes d'impulsions généralisées $p_1,...,p_i,...$ avec $i=1,2,...,n$ , si le système étudié possède $n$ degrés de liberté. Soit par exemple l'énergie cinétique $K$ et l'énergie potentielle $V$ d'une particule données par :

$K={{1}\over{2m}}(P_x^2+P_y^2+P_z^2)~~~~~~~~~~~~~~~~~~~~~~~~~~~~V=V(x,y,z)$

et les composantes de son moment cinétique :

$L_x=yp_z-zp_y~~~~~~~~~~~~~~~~~~~~~~~~~~L_y=zp_x-xp_z~~~~~~~~~~~~~~~~~~~~~~~~~~L_z=xp_y-yp_x$

A titre de complément de l'énoncé du postulat II, nous admettrons que les relations algébriques, et notamment les relations de définition, des grandeurs physiques, qui, en mécanique classique, ne font pas intervenir de dérivées, sont aussi satisfaites par les opérateurs quantiques images.

Par suite si les variables dynamiques classiques $\hat{A},\hat{B},\ldots,\hat{Z},\hat{\Omega}$ sont liées par une relation algébrique :

$\hat{\Omega}=f(\hat{A},\hat{B},\ldots,\hat{Z})$

alors les observables images satisfont la même relation :

$\Omega=f(A,B,\ldots,Z)$

En particulier une telle relation définit $\Omega$ comme fonction des observables $A,B,\ldots,Z$ .

Si l'énoncé précédent exclut la présence de dérivées, c'est que celles-ci ne sont pas transposables dans le codage mathématique. Par exemple, en ce qui concerne la grandeur force :

$$\hat{F}_x=-\frac{\partial\hat{V}}{\partial\hat{x}}~~ \not\rightarrow~~-{{\partial V}\over{\partial X}}$$

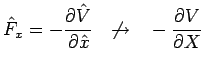car la dérivée par rapport à une observable n'est pas une opération définie. De même en ce qui concerne la grandeur vitesse :

$$\hat{V}_x=\frac{d\hat{X}}{dt}~~\not\rightarrow~~-{{dX}\over{dt}}$$

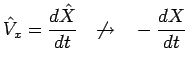car la grandeur physique mesurable $\hat{X}$ est codée, dans le formalisme, par une observable $X$ (opérateur linéaire hermitique) qui est bien définie, toujours la même, et qui ne dépend pas du temps $t$ . Ainsi des grandeurs physiques, telles la force et la vitesse ne sont plus codables, ni transposables dans le formalisme quantique, et les concepts correspondants^I30 doivent être abandonnés !

Toutefois, la règle de transposition précédente :

$\hat{\Omega}=f(\hat{A},\hat{B},\ldots,\hat{Z})~~~\longrightarrow~~~ \Omega=f(A,B,\ldots,Z)$

laisse subsister une ambiguïté. En effet, les grandeurs physiques classiques $\hat{A},\hat{B},\ldots$ commutent tandis que leurs images quantiques $A,B,\ldots$ peuvent ne pas commuter, de sorte que deux expressions classiques équivalentes :

$\hat{A}.\hat{B}=\hat{B}.\hat{A}$

admettraient deux codages bien distincts :

$A.B\not=B.A$

Il y a donc lieu de préciser qu'avant transposition quantique les expressions classiques doivent être symétrisées de telle sorte que, par exemple, dans le cas précédent :

$$\hat{A}.\hat{B}={{\hat{A}\hat{B}+\hat{B}\hat{A}}\over{2}}~~ \longrightarrow~~{{1}\over{2}}(AB+BA)$$

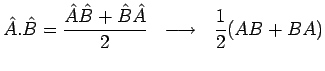Si $F(\hat{A})$ est une fonction polynômiale d'une variable dynamique physique $\hat{A}$ , l'observable $F(A)$ image de $F(\hat{A})$ se déduit immédiatement de l'observable $A$ image de $\hat{A}$ :

$$F(\hat{A})=\sum\limits_{i=1}^n a_i \hat{A}^i~~\longrightarrow~~ F(A)=\sum\limits_{i=1}^n a_i A^i$$

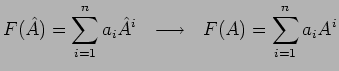car les sommes et produits d'opérateurs ont déjà été définis. Il n'en est pas de même si par exemple :

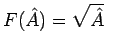$F(\hat{A})=\sqrt{\hat{A}}~~$ ou $~~F(\hat{A})=e^{\hat{A}}$

car la racine carrée ou l'exponentielle d'une observable n'ont pas encore été définies. Une définition de $F(A)$ devient alors nécessaire.

D'une façon générale, $F(A)$ sera définie comme un opérateur linéaire, dont l'action sur le ket $\mid g>$ quelconque est alors elle-même définie par son action sur les vecteurs d'une base. Il y a avantage à choisir la base constituée des vecteurs propres ${\mid a,x>}$ de l'observable $A$ :

Avec $\mid g>=\underset{a,x}{\scalebox{1.7}{S}}~g(a,x)~\mid a,x>~~~~F(A)\mid g>=\underset{a,x}{\scalebox{1.7}{S}}~g(a,x)~F(A)~\mid a,x>$

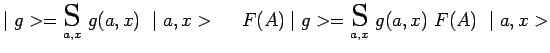
et par définition de $F(A)$ :

$F(A)~\mid a,x>=F(a)~\mid a,x>$

On en déduit immédiatement les expressions de l'action de $F(A)$ dans les cas de :