Le principe de Pauli trouve son application la plus simple, quand on
considère un ensemble de particules identiques, indépendantes, ou soumises à
un champ de forces extérieur commun. A titre d'exemple, considérons l'ensemble
des électrons d'un atome, quand l'effet global des interactions mutuelles
entre ces électrons est schématisé par celui d'un potentiel central moyen
![]() . Les électrons sont alors considérés comme s'ils étaient
indépendants. Chacun d'entre eux est plongé dans le même potentiel, et
donc admet le même hamiltonien, de telle sorte que le hamiltonien total
s'écrit dans la représentation de Schrödinger :
. Les électrons sont alors considérés comme s'ils étaient
indépendants. Chacun d'entre eux est plongé dans le même potentiel, et
donc admet le même hamiltonien, de telle sorte que le hamiltonien total
s'écrit dans la représentation de Schrödinger :
![$\displaystyle H=\sum\limits_{i=1}^n\,h_i=
\sum\limits_{i=1}^n\,\left[\,\frac{-\hbar^2}{2m}\,\Delta_i+V(r_i)\,\right]$](img3655.png) |
![]() désignant les trois coordonnées spatiales du
désignant les trois coordonnées spatiales du
![]() électron. On obtient les fonctions
propres de
électron. On obtient les fonctions
propres de ![]() en cherchant celles de l'hamiltonien individuel commun :
en cherchant celles de l'hamiltonien individuel commun :
![]() désignant l'une des valeurs propres du spectre
correspondant aux états quantiques d'un électron. En effet avec :
désignant l'une des valeurs propres du spectre
correspondant aux états quantiques d'un électron. En effet avec :
Question 5-6 : Vérifiez l'équation précédente en y portant
l'expression de ![]() , et en divisant ensuite les deux membres par
, et en divisant ensuite les deux membres par ![]() .
.
La dégénérescence d'échange est alors manifeste puisque toutes les
fonctions de la forme :
obtenues en distribuant arbitrairement les variables
![]() dans les parenthèses laissées vides,
on obtient une nouvelle fonction propre, relative à la même valeur propre
dans les parenthèses laissées vides,
on obtient une nouvelle fonction propre, relative à la même valeur propre
![]() . Puisque le spin des électrons est demi-entier (
. Puisque le spin des électrons est demi-entier (
![]() ) la
fonction solution physique doit être antisymétrique. Aucune des solutions
mathématiques précédentes ne l'est, et donc aucune n'est acceptable
seule, pour solution physique, mais on peut former une combinaison linéaire
antisymétrique de ces solutions particulières, qui sera la solution physique :
) la
fonction solution physique doit être antisymétrique. Aucune des solutions
mathématiques précédentes ne l'est, et donc aucune n'est acceptable
seule, pour solution physique, mais on peut former une combinaison linéaire
antisymétrique de ces solutions particulières, qui sera la solution physique :
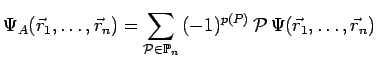 |
![]() désignant une quelconque des
solutions mathématiques précédentes et par exemple :
désignant une quelconque des
solutions mathématiques précédentes et par exemple :
En effet, on remarque que ![]() peut alors s'écrire sous la forme d'un
déterminant de fonctions, appelé déterminant de Slater :
peut alors s'écrire sous la forme d'un
déterminant de fonctions, appelé déterminant de Slater :
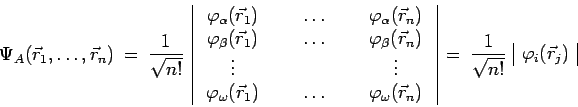 |
L'indice de ligne
![]() désigne la suite
des
désigne la suite
des ![]() états occupés chacun par une particule. L'indice de colonne
états occupés chacun par une particule. L'indice de colonne
![]() repère la suite des
repère la suite des ![]() coordonnées
coordonnées
![]() des
des ![]() électrons. On vérifie bien,
en effet, que ce déterminant jouit bien sous l'effet des permutations des
particules, c'est-à-dire de ses colonnes, de toutes les propriétés d'antisymétrie
imposées par le principe de Pauli.
électrons. On vérifie bien,
en effet, que ce déterminant jouit bien sous l'effet des permutations des
particules, c'est-à-dire de ses colonnes, de toutes les propriétés d'antisymétrie
imposées par le principe de Pauli.
Question 5-7 : Justifiez le facteur de normalisation
![]() en démontrant que
en démontrant que ![]() est normée si les fonctions individuelles
est normée si les fonctions individuelles
![]() le sont également (ce que nous supposons toujours).
le sont également (ce que nous supposons toujours).