Exponentielle du hamiltonien

Certaines des expressions précédentes de l'opérateur évolution sont des exponentielles de l'observable $H$ . Précédemment^VI1 ce type de fonction d'observable a été défini au moyen de son développement en série :

$$e^A = 1 + \frac{A}{1} +\frac{A^2}{2!} +\frac{A^3}{3!} + \ldots + \frac{A^n}{n!} + \ldots$$

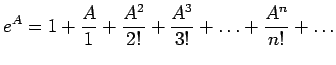Or, bien qu'un tel développement soit toujours convergent si $A$ désigne un nombre, il n'en est pas de même si $A$ désigne un opérateur.

Considérons en effet le cas particulier :

$$\Psi(x,0)=(\sigma\sqrt{2\pi})^{-\frac{1}{2}}\,e^{-\scalebox{1.2}{... ...ac{x^2}{4\sigma^2}$}}~~~~~~ \mathrm{et}~~~H=-\frac{\hbar^2}{2m}\,\frac{d}{dx^2}$$

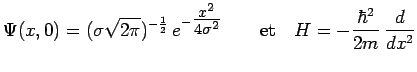A l'instant $t$ et pour $x=0$ , on obtient alors :

$$\Psi(0,t)=(\sigma\sqrt{2\pi})^{-\frac{1}{2}}\,\left( \mathcal{U}(t)\,e^{-\scalebox{1.2}{$\frac{x^2}{4\sigma^2}$}}\right)_{x=0}$$

$$\Psi(0,t)=(\sigma\sqrt{2\pi})^{-\frac{1}{2}}\, \sum\limits_n\,\left(\frac{i\hbar t}{8m\sigma^2}\right)^n\, \frac{(2n!)}{n!\,n!}\,(-1)^n$$

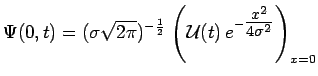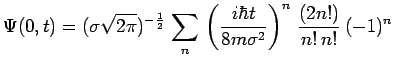et cette dernière somme diverge pour $t\rightarrow\infty$ puisque le critère de convergence s'écrit :

$$\lim_{n\to\infty}~\left\vert~\frac{i\hbar t}{8m\sigma^2}~\frac{(2n+1)(2n+2)}{(n+1)(n+1)}~\right\vert\leq 1$$

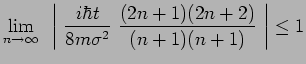et n'est pas satisfait quel que soit $t$ .

Le développement traditionnel de l'exponentielle d'observable n'est donc pas toujours efficient quand on l'applique à une fonction d'onde quelconque. Par contre, si cette dernière est préalablement développée sur la base constituée des états propres d'énergie $\vert E_k>$ l'action de l'opérateur d'évolution $\mathcal{U}(t-t_0)$ est toujours bien définie.

Dans le cas de l'exemple ici considéré d'une particule libre :

$$\vert E_k>=\vert k>~~~~~<x\vert E_k>=h^{-\frac{1}{2}}\,e^{ikx}~~~~~~ E_k=\frac{\hbar^2k^2}{2m}$$

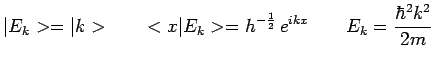et on obtient successivement, en omettant des facteurs constants :

$$\vert\Psi(0)> = \int_{-\infty}^{+\infty}\,\vert k>\,dk\,<k\vert\Psi(0)>$$

$$\mathcal{U}(t)\vert\Psi(0)> = \int_{-\infty}^{+\infty}\,e^{-\frac{i}{\hbar}\,Ht}\vert k>\,dk\,<k\vert\Psi(0)>$$

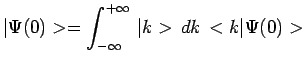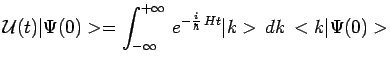et puisque :

$$H\,\vert k>=E_k\,\vert k>=\frac{\hbar^2k^2}{2m}\,\vert k>$$

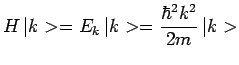alors :

$$\Psi(x,t) = <x\vert\,\mathcal{U}(t)\,\vert\Psi(0)> = \frac{1}{\sq... ..._{-\infty}^{+\infty}\, e^{ikx}\,e^{-i\,\frac{\hbar^2k^2}{2m}\,t}\,\Psi_0(k)\,dk$$

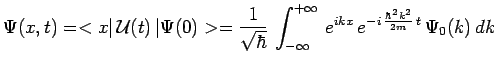Cette dernière intégrale est convergente et conduit au résultat :

$$\Psi(x,t) = C^{te}\,\left(1+\frac{i\hbar t}{2m\sigma^2}\right)^{-... ...ac{x^2}{4\sigma^2}$}}{1+i\,\scalebox{1.4}{$\frac{\hbar t}{2m\sigma^2}$}}\right)$$

d'où :

$$\vert\Psi(x,t)\vert^2 = C^{te}\,\left(1+\frac{\hbar^2 t^2}{4m\sig... ...{x^2}{2\sigma^2}$}}{1+\scalebox{1.4}{$\frac{\hbar^2 t^2}{4m\sigma^4}$}}}\right)$$

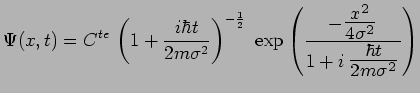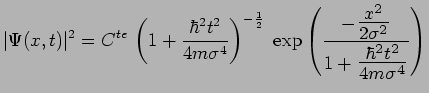d'où résulte l'étalement du paquet d'ondes puisque :

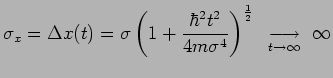$$\sigma_x=\Delta x(t) = \sigma\left(1+\frac{\hbar^2 t^2}{4m\sigma^4}\right)^{\frac{1}{2}}~ \underset{t\rightarrow\infty}{\longrightarrow}~\infty$$