![]() - Nécessairement
- Nécessairement
![]()
![]() - Si
- Si ![]() alors
alors
![]() . Si
. Si
![]() alors
alors
![]() est vecteur propre de
est vecteur propre de ![]() correspondant à la valeur propre
correspondant à la valeur propre ![]() et de norme
et de norme
![]()
![]() -
-
![]() n'est pas nul. Sa
norme est
n'est pas nul. Sa
norme est
![]() et c'est un vecteur propre de
et c'est un vecteur propre de
![]() correspondant à la valeur propre
correspondant à la valeur propre ![]() .
.
En effet, par hypothèse :
et on en déduit les normes de
![]() et de
et de
![]() :
:
Or la norme d'un vecteur de l'espace de Hilbert est positive ou
nulle et la nullité de la norme est la condition nécessaire et
suffisante de celle du vecteur. Pour que cet axiome soit ici
satisfait, il faut et il suffit que l'on ait :
et si ![]() il en résulte :
il en résulte :
Par ailleurs
![]() puisque :
puisque :
Enfin
![]() et
et
![]() vérifient
bien les équations aux valeurs propres annoncées puisque :
vérifient
bien les équations aux valeurs propres annoncées puisque :
A partir d'un vecteur propre ![]() quelconque, on peut
construire une suite d'autres vecteurs propres :
quelconque, on peut
construire une suite d'autres vecteurs propres :
correspondant respectivement aux valeurs propres :
Puisque la suite des valeurs propres est bornée
inférieurement par 0
, il doit donc nécessaire-ment
exister un vecteur noté ![]() et tel que :
et tel que :
| 0 |
A partir de ce vecteur ![]() on peut alors engendrer tous les
autres vecteurs propres par action de l'opérateur
on peut alors engendrer tous les
autres vecteurs propres par action de l'opérateur
![]() . On obtiendra ainsi la suite :
. On obtiendra ainsi la suite :
correspondant respectivement aux valeurs propres :
L'observable ![]() constitue alors, à elle seule, un ensemble
complet d'observables qui commutent car aucune de ses valeurs
propres n'est dégénérée.
constitue alors, à elle seule, un ensemble
complet d'observables qui commutent car aucune de ses valeurs
propres n'est dégénérée.
On peut maintenant construire la suite des vecteurs propres
orthonormés de ![]() notés :
notés :
qui se déduisent les uns des autres par les
relations de récurrence :
| 0 |
Le vecteur propre de rang ![]() peut également s'écrire :
peut également s'écrire :
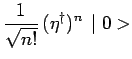 |
avec :
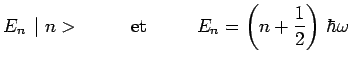 |