


suivant: B) Réfraction de la
monter: Réflexion et transmission de
précédent: 3) Sur un miroir
Table des matières
Afin de mieux mettre en évidence l'interférence destructrice
qui vient d'être signalée, il est utile de diviser par la
pensée un des éléments marginaux 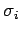 éloigné du point de réflexion classique I, en huit
parties suffisamment étroites
éloigné du point de réflexion classique I, en huit
parties suffisamment étroites
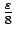 pour que
la variation
pour que
la variation
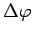 de la phase, dûe à la
différence
de la phase, dûe à la
différence
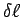 de chemin à parcourir et
correspondant à deux parties voisines de
de chemin à parcourir et
correspondant à deux parties voisines de 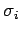 , soit de
l'ordre de
, soit de
l'ordre de
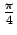 :
:
|
La somme vectorielle des huit contributions partielles est bien
nulle pour cet élément 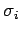 . Elle l'est presque
également aussi pour l'élément voisin
. Elle l'est presque
également aussi pour l'élément voisin
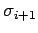 puisque
pour lui la relation précédente est presque également
satisfaite. Si donc on supprime, par grattage par exemple,
la même moitié réfléchissante de tous ces
éléments voisins
puisque
pour lui la relation précédente est presque également
satisfaite. Si donc on supprime, par grattage par exemple,
la même moitié réfléchissante de tous ces
éléments voisins 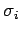 et
et
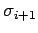 , (et on
réalise alors ce qui est appelé un réseau) chacune de ces
deux moitiés de ces deux éléments voisins apportera presque
la même contribution à l'amplitude totale de diffusion :
, (et on
réalise alors ce qui est appelé un réseau) chacune de ces
deux moitiés de ces deux éléments voisins apportera presque
la même contribution à l'amplitude totale de diffusion :
avec :
La lumière sera donc alors diffractée par tous ces
éléments dans une direction
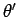 telle que la
condition de phase précédente soit satisfaite :
telle que la
condition de phase précédente soit satisfaite :
|
|
On remarque que
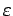 étant supposé fixé, la
direction
étant supposé fixé, la
direction
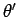 de diffusion dépend de
de diffusion dépend de 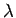 de
telle sorte que le réseau diffracte dans des directions
de
telle sorte que le réseau diffracte dans des directions
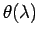 les diverses composantes d'une lumière blanche
incidente.
les diverses composantes d'une lumière blanche
incidente.
On notera que la condition de diffraction ne peut être
satisfaite que si
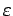 est de l'ordre de
est de l'ordre de 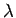 soit
donc :
soit
donc :
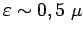 m pour la lumière visible et
m pour la lumière visible et
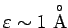 pour le rayonnement X.
pour le rayonnement X.
Dans ce dernier cas, la structure cristalline des solides
réalise des réseaux naturels et la condition
précédente s'appelle la condition de Bragg.



suivant: B) Réfraction de la
monter: Réflexion et transmission de
précédent: 3) Sur un miroir
Table des matières
Arnaud Balandras
2005-04-02
![]() éloigné du point de réflexion classique I, en huit
parties suffisamment étroites
éloigné du point de réflexion classique I, en huit
parties suffisamment étroites
![]() pour que
la variation
pour que
la variation
![]() de la phase, dûe à la
différence
de la phase, dûe à la
différence
![]() de chemin à parcourir et
correspondant à deux parties voisines de
de chemin à parcourir et
correspondant à deux parties voisines de ![]() , soit de
l'ordre de
, soit de
l'ordre de
![]() :
:

![]() est de l'ordre de
est de l'ordre de ![]() soit
donc :
soit
donc :
![]() m pour la lumière visible et
m pour la lumière visible et
![]() pour le rayonnement X.
pour le rayonnement X.