B) Réfraction de la lumière

Pour des raisons expliquées dans la suite, le vitesse de la lumière $v$ dans l'eau est plus faible que dans l'air $v=\scalebox{1.4}{$\frac{c}{n}$}$ ($n$ désignant l'indice de l'eau).

Cette circonstance permet d'expliquer le phénomène de réfraction. En effet, ici encore, les amplitudes $\vec{Z}_i$ associées aux éléments $\sigma_i$ s'ajoutent vectoriellement : $$\vec{Z} = \sum\,\vec{Z}_i$$ avec : $$Z_i = A\,e^{i\,\varphi_{i}}$$

et :

$$\frac{\varphi_i}{2\pi} = \frac{t_i}{T}$$

$$= \frac{1}{T}\,\left(\frac{l_i^{(1)}}{c}+\frac{l_i^{(2)}}{v}\right)$$

$$= \frac{1}{\lambda}\,\left(l_i^{(1)}+n\,l_i^{(2)}\right)$$

$$= \frac{1}{\lambda}\,O_i$$

La contribution des éléments $\sigma_i$ est maximum au voisinage d'un point J, là où la phase $\varphi_i$ est stationnaire, c'est-à-dire là où le chemin optique $O_i$ est minimum, conformément au principe de Fermat. Au contraire, loin du point J, la phase $\varphi_i$ varie rapidement et les contributions des éléments voisins s'annihilent mutuellement.

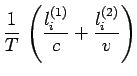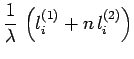On peut toutefois obtenir une contribution constructive de tous ces éléments $\sigma_i$ en faisant en sorte que les phases $\varphi_i$ soient égales. C'est ce qui est réalisé avec une lentille de verre.

Ici encore, l'amplitude totale $Z$ de probabilité associée au processus de détection du photon en R, quand il est émis en S, est égale à la somme cohérente des amplitudes partielles $Z_i$ correspondantes aux diverses voies : $$Z = \sum\,Z_i \;=\; \sum\,Z(\sigma_i)$$ L'amplitude $Z$ devient très grande quand les phases $\varphi_i$ deviennent égales entre elles, c'est-à-dire lorsque tous les éléments $\sigma_i$ correspondent au même chemin optique : $$l_i^{(1)}+n\,l_i^{(2)} = l_0^{(1)}+n\,l_0^{(2)} \;=\; \textrm{C}^{\textrm{te}}$$

La lumière émise par la source S est alors focalisée au point R pour lequel la condition de convergence précédente est satisfaite.