Pour aller d'un point ![]() d'émission à un autre point
d'émission à un autre point ![]() de détection, le photon est a priori susceptible de suivre
n'importe quel chemin
de détection, le photon est a priori susceptible de suivre
n'importe quel chemin ![]() . L'amplitude associée à un tel
chemin peut encore s'écrire, conformément au modèle
schématique utilisé jusqu'ici :
. L'amplitude associée à un tel
chemin peut encore s'écrire, conformément au modèle
schématique utilisé jusqu'ici :
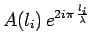 |
et la probabilité du processus ![]() est encore
une somme cohérente des contributions des différents
chemins
est encore
une somme cohérente des contributions des différents
chemins ![]() :
:
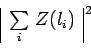 |
Toutefois, le bon chemin ![]() , c'est-à-dire celui qui est
observé expérimentalement, est le chemin le plus
probable. C'est celui au voisinage duquel les contributions des
chemins voisins s'ajoutent algébriquement ou vectoriellement
d'une façon constructive. Ici encore ce chemin
, c'est-à-dire celui qui est
observé expérimentalement, est le chemin le plus
probable. C'est celui au voisinage duquel les contributions des
chemins voisins s'ajoutent algébriquement ou vectoriellement
d'une façon constructive. Ici encore ce chemin ![]() est celui
pour lequel la phase
est celui
pour lequel la phase ![]() , et donc tout simplement aussi
, et donc tout simplement aussi ![]() ,
sont stationnaires. Ce chemin est la ligne droite
,
sont stationnaires. Ce chemin est la ligne droite ![]() pour
laquelle la longueur est minimum.
pour
laquelle la longueur est minimum.
On notera toutefois que ce bon chemin n'est affecté d'une probabilité appréciable que si il est entouré d'un nombre suffisant de chemins voisins pour que la somme algébrique de leurs contributions soit elle-même suffisante.
|
|