Expressions des opérateurs de moment cinétique

Les expressions, dans la base sphérique $\{r,~\theta,~\varphi\}$ des opérateurs de moment cinétique se déduisent de leurs expressions écrites dans la base cartésienne $\{x,~y,~z\}$ . Il s'agit là d'un problème de changement de variables dans les dérivées partielles :

$$L_z = XP_y-YP_x ~=~ \frac{\hbar}{i}\,(x\partial_y-y\partial_x) ~=~ \fra... ...ar}{i}\,\frac{\partial}{\partial_\varphi} ~=~ \frac{\hbar}{i}\,\partial_\varphi$$

$$L_\pm = L_x\pm iL_y ~=~ \hbar\,e^{\pm i\varphi}\,(\pm\partial_\theta+i\cot\theta\,\partial_\varphi)$$

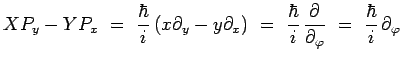Il en résulte alors avec :

$$\vec{L}^{\,2} = \frac{1}{2}\,(L_+L_-+L_-L_+)+L_z^2$$

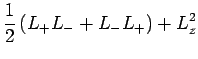$$\vec{L}^{\,2} = \frac{-\hbar^2}{\sin^2\theta}\,\left[\sin\theta\,\partial_\theta(\sin\theta\,\partial_\theta)+\frac{\partial^2}{\partial\varphi^2}\right]$$

Puisque les variables $\theta$ et $\varphi$ sont indépendantes, on vérifie bien la relation de commutation :

$$[\vec{L}^{\,2},L_z] =$$ 0

Il est essentiel de remarquer que tous les opérateurs de moment cinétique $L_x~L_y~L_z~L_+~L_-$ et $\vec{L}^{\,2}$ n'agissent que sur les variables $\theta$ et $\varphi$ . Par suite, les fonctions propres de ces opérateurs seront des fonctions des seules variables $\theta$ et $\varphi$ .