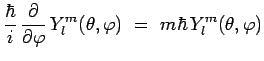 |
De la relation de définition :
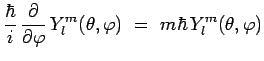 |
on en déduit immédiatement :
d'où en particulier pour ![]() :
:
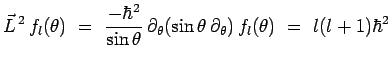 |
Avec :
et la fonction ![]() est solution de l'équation
différentielle :
est solution de l'équation
différentielle :
![$\displaystyle \left[ (1-u^2)\, \frac{d^2}{du^2} -2u\,\frac{d}{du} + l(l+1)\right]\,f_l(u)$](img2310.png) |
0 |
soit :
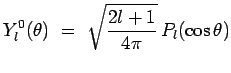 |
![]() désignant le
désignant le
![]() polynôme de Legendre :
polynôme de Legendre :
 |
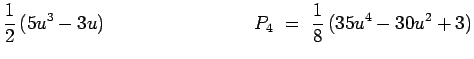 |
La fonction harmonique sphérique la plus générale est
solution de l'équation aux dérivées partielles suivante :
![$\displaystyle -\hbar^2\,\left[ \frac{1}{\sin\theta}\,\partial_\theta\,(\sin\the...
...+ \frac{1}{\sin^2\theta}\,\partial^2_{\varphi^2} \right]\,Y^m_l(\theta,\varphi)$](img2320.png) |
|||
ou encore, tenu compte d'un résultat précédent :
![$\displaystyle \left[ (1-u^2)\,\frac{d^2}{du^2} -2u\,\frac{d}{du} -\frac{m^2}{1-u^2} + l(l+1)\right]\,f^m_l(u)$](img2323.png) |
0 |
Tenu compte des relations d'orthonormalisation et en choisissant
les phases de telle manière que les relations habituelles de
récurrence :
soient satisfaites, on obtient les expressions des premières harmoniques sphériques qui sont indiquées dans le tableau ci-après.
On démontre que toutes ces fonctions harmoniques sphériques
jouissent des propriétés de symétrie suivantes :