Il suffit maintenant de mettre en correspondance les deux
expressions du nombre ![]() d'événements détectés par
un appareillage qui sélectionne les états finals
d'événements détectés par
un appareillage qui sélectionne les états finals
![]() :
:
![]() la première qui est d'origine expérimentale et qui
définit la notion de section efficace différentielle
la première qui est d'origine expérimentale et qui
définit la notion de section efficace différentielle
![]() :
:
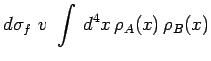 |
![]() la seconde qui exprime les hypothèses et un
modèle théorique d'interaction sous forme des éléments
la seconde qui exprime les hypothèses et un
modèle théorique d'interaction sous forme des éléments
![]() de la matrice réduite
de la matrice réduite
![]() d'interaction :
d'interaction :
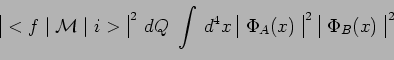 |
d'où finalement en tenant compte de la relation entre
![]() et
et ![]() :
:
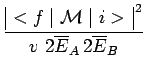 |
Le dénominateur du second membre peut encore s'écrire sous une
forme générale invariante relativiste :
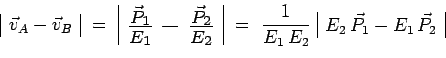 |
et si
![]() (choc de plein fouet) :
(choc de plein fouet) :
la dernière égalité étant valable seulement dans
le référentiel du centre de masse :
et
![]() désignant le
produit des deux 4-vecteurs.
désignant le
produit des deux 4-vecteurs.
D'où le résultat final :
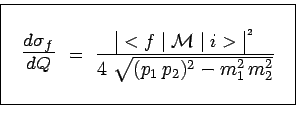 |
On notera que ![]() ,
, ![]() et
et
![]() sont
également chacun des invariants relativistes.
sont
également chacun des invariants relativistes.